УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ ИДЕАЛЬНОЙ ЖИДКОСТИ

Вторым основным уравнением гидродинамики является урав­нение Бернулли, устанавливающее зависимость между скоростью и давлением в различных сечениях одной и той же струйки. При выводе этого уравнения также ограничимся случаем установив­шегося медленно изменяющегося движения.

Рис .30

Выделим в пространственной элементарной струйке объем, ограниченный в некоторый момент времени Т сечениями 1—1 и 2—2, нормальными к оси струйки О_г0₂ (рис. 30). Первоначально будем считать жидкость идеальной, т. е. лишенной вязкости. Силы внутреннего трения в такой жидкости отсутствуют, и к выделен­ному объему струйки приложены только силы тяжести и силы гидродинамического давления. Пусть за некоторый малый про­межуток времени ΔТ указанный объем переместится в положе­ние 1'—1', 2'—2'. Применим к его движению теорему кинетической энергии (называемую также теоремой живых сил), согласно которой приращение кинетической энергии (живой силы) движу­щейся системы материальных, частиц равняется сумме работ всех сил, действующих на систему. Эта теорема может быть выра­жена следующим уравнением:

ΔW =ΣA [81]

где ΔW - приращение кинетической энергии; ΣA— сумма ра­бот действующих сил (напомним, что выражение для кинетической энергии материальной точки имеет вид

W = m υ ²/2 , а для работы — А = РΔS ; в этих выражениях т — масса, υ — ско­рость материальной точки, Р — равнодействующая сил, прило­женных к точке; ΔS — проекция элементарного перемещения точки на направление силы).

В рассматриваемом случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т. е. как разность кине­тической энергии объема V_1'-2 и объема V_1-2. Замечая, что объем V_1'-2 входит как составная часть в выражения для объемов V_1-2 и V_1'-2':

V_1-2 = V_1-1' + V_1'-2

V_1'-2' = V_1'-2 + V_2-2'

и имея в виду, что кинетическая энергия объема V_1'-2 при уста­новившемся движении жидкости одинакова как в момент вре­мени Т, так и в момент Т + ΔТ, приходим к выводу, что искомое приращение кинетической энергии в конечном счете определится разностью кинетической энергии объемов V_2-2' V_1-1'. Назван­ные объемы являются результатом перемещения за время ΔT торцевых сечений выделенного участка элементарной струйки. Обозначая скорость в сечении 1-1 через υ ₁, в сечении 2—2 че­рез υ ₂, получаем, что соответствующие перемещения будут равны υ ₁ΔT и υ ₂ΔТ, а рассматриваемые объемы

V_1-1' = ΔF₁ υ ₁ΔT = q₁ΔT ; V_2-2'= ΔF₂ υ ₂ΔT = q₂ΔT, где q₁ ,q₂ значения расхода в сечениях 1-1 и 2-2.

Но по условию неразрывности расход во всех сечениях эле­ментарной струйки одинаков (q₁ = q₂ = q), и следовательно, V_1-1' = V_2-2' = qΔT масса же рассматриваемых объемов m = ρqΔT

Таким образом, выражение для приращения кинетической энергии можно записать в виде 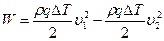или

Перейдем теперь к определению работы сил, действующих на рассматриваемый объем жидкости. Работа силы тяжести равна произведению этой силы на путь, пройденный

точкой ее прило­жения, т. е. центром массы (тяжести) движущегося объема жид­кости по вертикали. Рассматривая, как и ранее, выделенный объем струйки в двух его положениях состоящим из объема V_1-2' и равных между собой объемов V_1-1' и V_2-2' легко прийти к за­ключению, что работа А_тсил тяжести в данном случае будет равна произведению силы тяжести объема V_1-1' г на расстояние z₁ – z₂ по вертикали между центрами масс объемов V_1-1' и V_2-2' т. е. А_т = mgZ₁ – mgZ₂, где Z₁ и Z₂ — расстояния по вертикали от произвольной горизон­тальной плоскости, называемой плоскостью сравнения до центров масс объемов V_1-1' = V_2-2' (или, иначе, вертикальные коорди­наты центров масс этих объемов).

Силы давления, действующие на объем жидкости, складываются из сил давления на его боковую поверхность и на концевые по­перечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы во все время движения нормальны

к перемещению их точек приложения. Сумма же работ сил давле­ния ΣA_д на торцевые сечения составит ΣА_д = Р₁ΔF₁ΔS₁ – P₂ΔF₂ΔS₂

где Р₁ΔF₁ – P₂ΔF₂— сила давления на торцы 1—1 и 2—2, а ΔS₁ и ΔS₂ — элементарные перемещения точек приложения этих сил за время ΔТ (работа сил давления на торец 2 отрицательна, так как направление силы р₂ ΔF₂ противоположно перемещениюΔS₂). Но величины ΔF₁ΔS₁ и ΔF₂ΔS₂ есть равные между собой объемы V_1-1' = V_2-2' массы m поэтому учитывая, что m = ρV_1-1' = ρV_2-2' выражение для суммы ΣA_д можно пред­ставить в виде

Подставляя найденные выражения для работ сил и для приращения кинетической энергии в уравнение [78] (Δ W =ΣA), получим

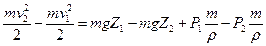
Разделим затем это уравнение на m =ρqΔT, т. е. отнесем его к единице массы протекающей жидкости, и перегруппируем члены. В результате будем иметь [82]

Учитывая, что сечения. 1—1 и 2—2 были взяты нами совер­шенно произвольно, это уравнение оказывается возможным рас­пространить на всю струйку, применив его для любых поперечных сечений, взятых по ее длине, и представить в более общем виде

[83]

Уравнения (3.12) и (3.13) представляют собой уравнение Бер­нулли для элементарной струйки идеальной жидкости. Сумма трех слагаемых, входящих в это уравнение, называется полной удель­ной энергией жидкости в данном сечении струйки и обозначается э. Различают удельную энергию положения gZ, удельную энергию давления р/ρ и кинетическую удельную энергию υ²/2.

В соответствии с этим уравнение Бернулли можно сформули­ровать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т. е. сумма удельной энергий положения, удельной энергии давления и кинетической удельной энергии, есть величина постоянная во всех сечениях струйки.