Дифференциальные уравнения равновесия жидкости (уравнения Эйлера).

Выделим в жидкости элементарный параллелепипед с ребрами dx, dy, dz, параллельными соответствующим осям координат (рис ниже). Масса жидкости в параллелепипеде равна ρdxdyd. Отбросим жидкость, окружающую параллелепипед, и заменим действие отброшенной жидкости силами. Это будут сжимающие поверхностные силы давления. Кроме поверхностных сил на жидкость действуют массовые силы fdW. Плотность распределения массовых сил f, ее проекции на координатные оси fх, fy, fz.

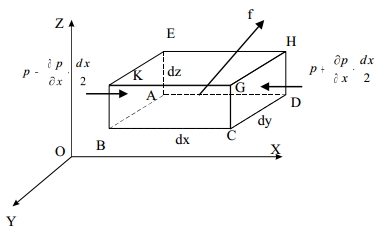
Пусть давление в центре объема равно p. Тогда для давления в центре граней ABKE и DCGH можно соответственно записать:

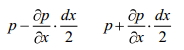
По второму закону Ньютона составим уравнение равновесия параллелепипеда вдоль оси OX:

раскрывая скобки и сокращая, получаем:

Записывая аналогичные уравнения для осей OY и OZ, получим:

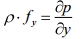
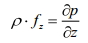
Данные уравнения называются уравнениями равновесия Эйлера.

В ЛЕКЦИЯХ ВОТ ТАКОЕ УРАВНЕНИЕ: