Сила давления жидкости на плоскую стенку. Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом, определяется по основному уравнению гидростатики Р=Р0+hρg

Определим силу F давления, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.

Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в плоскости стенки.

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS (давление действующее в точке, одинаково для произвольно расположенной площадки) dFж = P*dS =(P₀ + ρhg)dS = P₀*dS + ρhg*dS,

где Р₀ — давление на свободной поверхности, h — глубина расположения площадки dS. Для определения полной силы Fж проинтегрируем полученное выражение по всей площади S:

,

где у — координата площадки dS, h = у*Sinα .

Последний интеграл 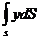представляет собой статический момент площади S относительно оси Ох и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.

Следовательно, Fж = P₀S+ρg(y_c Sinα) S = P₀S+ρgh_cS (3.11)

здесь h_c = (Sinα)y_c — глубина расположения центра тяжести площади S, или