
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЖИДКОСТИ В ЦИЛИНДРИЧЕСКОМ СОСУДЕ, РАВНОМЕРНО ВРАЩАЮЩЕМСЯ ВОКРУГ ВЕРТИКАЛЬНОЙ ОСИ
Основы теории и цель работы
Относительным равновесием жидкости называется такое состояние, при котором отдельные ее частицы не смещаются одна относительно другой, а также стенок сосуда - и вся масса жидкости движется как твердое тело.
В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести. При относительном покое к ней добавляется еще массовая сила – сила инерции.
Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
При изучении относительного равновесия необходимо заниматься, во-первых, установлением закона распределения давления внутри жидкости, а, во-вторых, определением формы поверхности равного давления, т.е. такой поверхности, все точки которой испытывают одинаковое давление.
Первая задача решается с помощью дифференциального уравнения гидростатики, справедливого для всех случаев равновесия
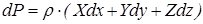 (3.1)
(3.1)
Вторая задача - с помощью дифференциального уравнения поверхности равного давления
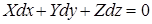 , (3.2)
, (3.2)
где x, y, z- координаты точек жидкости в системе отсчета, связанной с аппаратом (сосудом); P=f(x,y,z) - давление в жидкости; r - плотность жидкости; X, Y, Z- проекции единичной массовой силы q на оси координат.
При движении сосуда в поле сил тяжести вектор единичной массовой силы 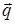 в каждой точке жидкости представляет собой сумму единичной силы тяжести
в каждой точке жидкости представляет собой сумму единичной силы тяжести  и единичной силы инерции
и единичной силы инерции  переносного движения:
переносного движения:
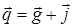 ;
;  , (3.3)
, (3.3)
где  - переносное ускорение в точке жидкости.
- переносное ускорение в точке жидкости.

 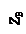  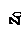 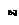  |
В случае относительного равновесия жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью
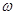 (рис. 3.1), вектор массовой силы
(рис. 3.1), вектор массовой силы 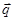 находится как сумма вектора
находится как сумма вектора
единичной силы тяжести  и вектора единичной центробежной силы инерции
и вектора единичной центробежной силы инерции 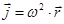 . Проекции
. Проекции 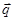 на оси координат представляются выражениями
на оси координат представляются выражениями
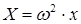 ;
;  ;
; 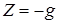 (3.4)
(3.4)
Интегрирование уравнений (3.1) и (3.2) с учетом зависимостей (3.4) дает, во-первых, закон распределения давления в жидкости
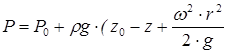 ) (3.5)
) (3.5)
и, во-вторых, уравнение свободной поверхности жидкости, которое имеет вид параболоида вращения
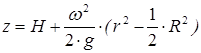 , (3.6)
, (3.6)
где P- давление в точке жидкости с координатами r и z; 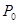 - давление на свободную поверхность жидкости в сосуде;
- давление на свободную поверхность жидкости в сосуде;  - координата вершины параболоида (рис. 3.1); R - радиус сосуда; H - уровень воды в сосуде при
- координата вершины параболоида (рис. 3.1); R - радиус сосуда; H - уровень воды в сосуде при  .
.
Из уравнения (3.6) при r=0 определяется координата вершины параболоида
 , (3.7)
, (3.7)
а при r=R координата верхней кромки параболоида
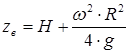 (3.8)
(3.8)
Из зависимости (3.8) можно определить максимальную угловую скорость вращения сосуда, при которой жидкость не будет переливаться из него, т.е., когда 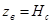
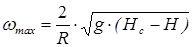 , (3.9)
, (3.9)
где 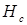 - высота сосуда.
- высота сосуда.
Цель работы- экспериментальное определение формы свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью, и сравнение результатов измерений с теоретическими расчетами.
Описание установки
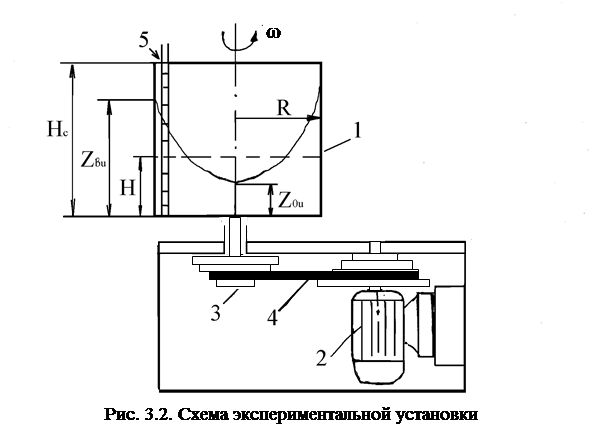
Вертикальный цилиндрический прозрачный сосуд 1 (радиусом R= 0,11 м и высотой 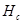 = 0,22 м) заполняется водой и приводится во вращение с помощью электродвигателя 2 (рис. 3.2) и ременной передачи со ступенчатыми шкивами 3. Для вращения сосуда 1 с разными скоростями ремень 4 перемещается вдоль ступенчатых шкивов 3. Число оборотов сосуда 1 измеряется с помощью тахометра. Уровень воды в сосуде 1 измеряется линейкой 5.
= 0,22 м) заполняется водой и приводится во вращение с помощью электродвигателя 2 (рис. 3.2) и ременной передачи со ступенчатыми шкивами 3. Для вращения сосуда 1 с разными скоростями ремень 4 перемещается вдоль ступенчатых шкивов 3. Число оборотов сосуда 1 измеряется с помощью тахометра. Уровень воды в сосуде 1 измеряется линейкой 5.
Проведение опытов и измерения
1. Перед началом эксперимента измеряется уровень воды в сосуде 1 с помощью линейки 5 (рис. 3.2). Этот уровень рекомендуется устанавливать на отметке H=0,08¸0,1 м. Если H<0,07 м сосуд необходимо долить водой.
2. Устанавливается ремень 4 в одно из положений и включается электродвигатель 2. Выжидают некоторое время, пока жидкость в сосуде 1 не придет в состояние относительного равновесия и стабилизации формы свободной поверхности (параболоида вращения). После этого производятся следующие измерения:
- частота вращения сосуда n;
- координаты верхней кромки параболоида вращения zви
- 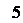




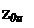 координаты вершины параболоида вращения zои.
координаты вершины параболоида вращения zои.

3. Измерения производятся для нескольких опытов с разными частотами вращения n. Все результаты измерений заносятся в табл. 3.1.
Вычисления и составление отчета
1. Определяется угловая скорость вращения сосуда по формуле
 , рад/с, (3.10)
, рад/с, (3.10)
где n – частота вращения сосуда, мин-1.
2. Вычисляются теоретические координаты кривой свободной поверхности жидкости в сосуде, а именно, координаты вершины параболоида z0 по формуле (3.7), а верхней кромки zв – по формуле (3.8).
3. По зависимости (3.9) определяется максимальная угловая скорость вращения сосуда w max.
4. Определяется степень отклонения (относительная погрешность) в % между измеренными и теоретическими координатами вершины и верхней кромки параболоида вращения по формулам
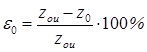 (3.11)
(3.11)
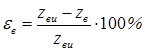 (3.12)
(3.12)
Все результаты вычислений заносятся в табл. 3.1.
5. По результатам измерений и вычислений строятся экспериментальная и теоретическая кривые свободной поверхности жидкости в меридиальном сечении сосуда (рис. 3.3). Промежуточные точки между z0 и zв теоретической кривой находятся по формуле (3.6), задаваясь значениями r. Экспериментальная кривая строится по трем точкам, т.е. по zои , zви и zR/2 при r=R/2=0,055 м, которая находится по зависимости



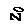
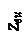
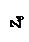

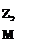
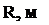
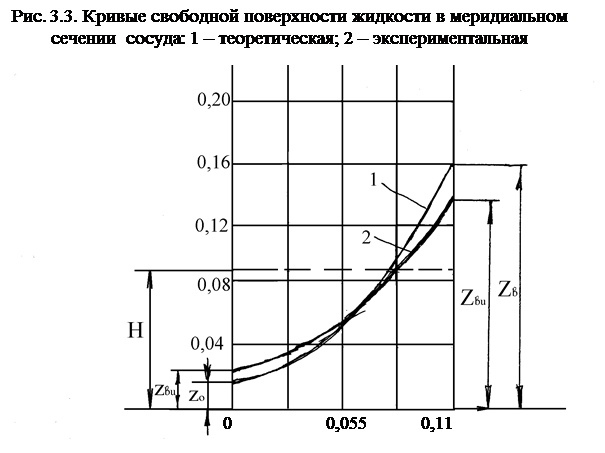 |
Таблица 3.1
.
| № опыта | Измеренные величины | Расчетные величины | ||||||||
| Высота уровня жидкости в сосуде H, м | Частота вращения сосуда n, мин-1 | Угловая скорость вращения сосуда w, рад/с | Координаты параболоида вращения | Максимальная угловая скорость вращения сосуда w max, рад/с | Координаты параболоида вращения | Относительная погрешность | ||||
| вершины Z0и, м | верхней кромки Zви, м | вершины Z0, м | верхней кромки Zв, м | e0, % | eв, % | |||||
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| 4. | ||||||||||
| 5. | ||||||||||
| 6. |
 , м (3.13)
, м (3.13)
Сравнение полученных кривых позволяет судить о том, насколько экспериментальная кривая свободной поверхности жидкости во вращающемся сосуде близка к теоретической кривой, т.е. к параболе.
В выводах следует отметить: какая форма свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью; причина образования параболоида вращения и его зависимость от частоты вращения сосуда; можно ли использовать и каким образом сосуд с жидкостью в качестве водяного тахометра.
Лабораторная работа № 4
Дата добавления: 2015-04-18; просмотров: 492; Мы поможем в написании вашей работы!; Нарушение авторских прав |