
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТРУБОПРОВОДА ПОСТОЯННОГО СЕЧЕНИЯ
Основы теории и цель работы
Потерями напора (энергии) по длине hl называются потери напора, обусловленные работой сил трения, равномерно распределенных (при равномерном движении) по всей длине потока. Применяя уравнение баланса энергии (уравнение Д. Бернулли) к общему случаю установившегося движения жидкости в трубопроводе постоянного сечения на участке длиной l между сечениями 1 и 2, получим
 , (6.1)
, (6.1)
где z1 и z2 - вертикальные координаты центров тяжести сечений; Р1 и Р2 – давление в центрах тяжести; 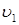 и
и  - средние скорости потока в сечениях 1 и 2;
- средние скорости потока в сечениях 1 и 2;  и
и 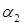 -значения коэффициента Кориолиса в соответствующих сечениях.
-значения коэффициента Кориолиса в соответствующих сечениях.
Так как кинематические характеристики в трубопроводе постоянного сечения равны по длине (  =
= 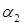 и
и 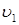 =
=  ), то скоростной напор (удельная кинетическая энергия потока) имеет одинаковую величину во всех ее сечениях
), то скоростной напор (удельная кинетическая энергия потока) имеет одинаковую величину во всех ее сечениях
 (6.2)
(6.2)
Из уравнения (6.1) с учетом (6.2), получаем
 (6.3)
(6.3)
Следовательно, потеря напора по длине равна уменьшению удельной потенциальной энергии (гидростатического напора) потока и определяется перепадом пьезометрических уровней в начальном и конечном сечениях данного участка трубопровода.
Уменьшение удельной энергии потока обусловлено ее диссипацией в теплоту при преодолении жидкостью гидравлических сопротивлений.
Гидравлические сопротивления по длине по роду сил подразделяются на обусловленные силой вязкости и связанные с инерцией массы жидкости, оказывающей сопротивление ускорению своего движения.
Вязкостное сопротивление возникает при относительном сдвиге слоев жидкости и является основным при ламинарном (слоистом) движении жидкости.
Силы трения по длине, отнесенные к единице площади, называются касательными напряжениями. Природа касательных напряжений, возникающих в турбулентном потоке, более сложная, чем в ламинарном. Кроме напряжений, обусловленных вязкостью жидкости, возникают еще напряжения, вызываемые поперечными перемещениями частиц жидкости. Исследователь турбулентности Буссинеск ввел понятие турбулентной вязкости. Он предложил касательные напряжения в турбулентном потоке при простом двухмерном движении определять по зависимости
 , (6.4)
, (6.4)
где  -динамическая вязкость жидкости;
-динамическая вязкость жидкости; 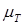 - динамическая турбулентная вязкость, зависящая от состояния турбулентного движения;
- динамическая турбулентная вязкость, зависящая от состояния турбулентного движения;  - осредненная местная скорость.
- осредненная местная скорость.
При ламинарном движении турбулентная вязкость равна нулю, при турбулентном 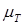 намного больше, чем
намного больше, чем  , поэтому последней можно пренебречь.
, поэтому последней можно пренебречь.
Инерционное сопротивление возникает в турбулентном потоке, в процессе преодоления инертности и ускорения отделившихся от стенки завихренных объемов жидкости. Их малая поступательная скорость увеличивается до величины, характерной для центральной части турбулентного потока с помощью потерянного напора.
Таким образом, потери по длине определяются действием вязкостных и инерционных сил сопротивления, доля участия которых в каждом конкретном случае зависит от режима движения жидкости, т.е. от числа Рейнольдса.
Так, при малых числах Рейнольдса (Re < Reкр), т.е. в условиях ламинарного режима, действием инерционных сил в механизме сопротивления можно пренебречь. Напротив, при развитом турбулентном режиме, т.е. при Re>>Reкр происходит практическое вырождение вязкостного сопротивления.
На характер механизма сопротивления при турбулентном режиме оказывает также значительное влияние пограничная геометрия потока, под которой в данном случае понимаются геометрические характеристики поверхности трубы (высота выступов шероховатости, их форма, взаимное расположение на поверхности и др.).
Поверхности стенок трубопроводов имеют различную шероховатость.
Высота выступов шероховатости называется абсолютной шероховатостью (  ). Так как промышленные трубопроводы обладают неравномерной высотой выступов, то пользуются понятием эквивалентной шероховатости, под которой понимают такую условно равномерную шероховатость, при которой потери напора в трубопроводе такие же, как и при естественной шероховатости. Эквивалентная шероховатость определяется при гидравлических испытаниях трубопроводов.
). Так как промышленные трубопроводы обладают неравномерной высотой выступов, то пользуются понятием эквивалентной шероховатости, под которой понимают такую условно равномерную шероховатость, при которой потери напора в трубопроводе такие же, как и при естественной шероховатости. Эквивалентная шероховатость определяется при гидравлических испытаниях трубопроводов.
Измерения скоростей показывают, что при переходе к турбулентному режиму у стенок сохраняется очень тонкий слой жидкости, в котором частицы, подторможенные и направленные стенками, сохраняют слоистый характер движения (так называемый ламинарный подслой). Поэтому профиль осредненных скоростей имеет два значительно различающихся участка (рис. 6.1). В турбулентном ядре благодаря интенсивному поперечному перемешиванию и выравниванию скоростей частиц осредненные скорости изменяются сравнительно слабо и их распределение по основной части сечения оказывается значительно более равномерным, чем при ламинарном режиме (ядро потока представляет так называемый турбулентный пограничный слой). В пределах ламинарного подслоя происходит весьма резкое падение скоростей от большого значения на его границе до нуля на стенке. Толщина  ламинарного подслоя чрезвычайно мала (сотые и тысячные доли диаметра трубопровода) и уменьшается с увеличением числа Рейнольдса.
ламинарного подслоя чрезвычайно мала (сотые и тысячные доли диаметра трубопровода) и уменьшается с увеличением числа Рейнольдса.
Между турбулентным ядром и ламинарным подслоем имеется тонкий переходной участок, в котором по мере приближения к подслою происходит резкое уменьшение турбулентных пульсаций и более интенсивное снижение осредненных скоростей. Поэтому, так как характеристики потока меняются по радиусу непрерывно, установить границы между этими участками можно только с известной условностью.
Приближенно толщину ламинарной пленки можно определить по формуле
 , (6.5)
, (6.5)
где 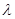 - коэффициент гидравлического трения; d- диаметр трубопровода;
- коэффициент гидравлического трения; d- диаметр трубопровода;
Если толщина ламинарного подслоя значительно больше высоты выступов шероховатости  (рис. 6.2, а), то они плавно обтекаются с очень малыми скоростями и, как в случае ламинарного движения, не влияют на распределение скоростей и сопротивление трения (область гидравлически гладких труб).
(рис. 6.2, а), то они плавно обтекаются с очень малыми скоростями и, как в случае ламинарного движения, не влияют на распределение скоростей и сопротивление трения (область гидравлически гладких труб).
По мере возрастания Re толщина ламинарного подслоя быстро уменьшается и становится близкой к высоте  выступов шероховатости. Последние при этом начинают выступать за пределы ламинарного подслоя и, вызывая дополнительные вихреобразования в потоке, начинают сказываться на величине гидравлического сопротивления, увеличивая турбулентность потока (область неполной шероховатости, рис. 6.2, б).
выступов шероховатости. Последние при этом начинают выступать за пределы ламинарного подслоя и, вызывая дополнительные вихреобразования в потоке, начинают сказываться на величине гидравлического сопротивления, увеличивая турбулентность потока (область неполной шероховатости, рис. 6.2, б).
 |  | ||
|
|
|


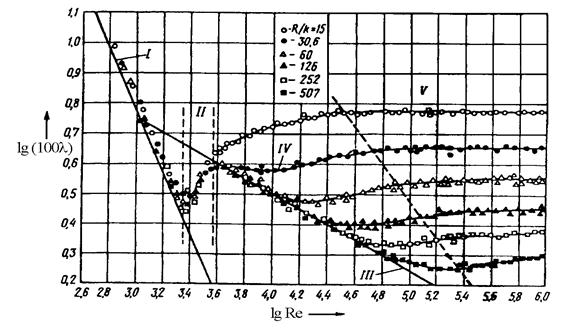
Рис. 6.3. Изменение коэффициента гидравлического сопротивления
при движении жидкости в круглой трубе в зависимости от числа
Рейнольдса и параметров искусственной (зернистой)
шероховатости (опытные данные И. Никурадзе).
При больших значениях Re толщина ламинарного подслоя становится настолько малой ( 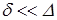 ), что выступы шероховатости почти полностью оказываются в турбулентном ядре потока (область гидравлически шероховатых труб, рис. 6.2, в). Обтекание выступов происходит с интенсивным отрывом вихрей, которые попадают в центральную часть потока и усиливают турбулентность. При этом влияние сил вязкости на гидравлическое сопротивление становится весьма малым, а основную роль играют инерционные силы.
), что выступы шероховатости почти полностью оказываются в турбулентном ядре потока (область гидравлически шероховатых труб, рис. 6.2, в). Обтекание выступов происходит с интенсивным отрывом вихрей, которые попадают в центральную часть потока и усиливают турбулентность. При этом влияние сил вязкости на гидравлическое сопротивление становится весьма малым, а основную роль играют инерционные силы.
Потери напора (энергии) по длине в трубопроводах определяются в общем случае по формуле Дарси-Вейсбаха, которая была получена эмпирическим путем в XIX веке
 , (6.6)
, (6.6)
где l и d – длина и диаметр трубопровода, м.
Из формулы (6.6) следует, что потери напора на трение при движении жидкости в трубопроводе возрастают с увеличением средней скорости потока и длины рассматриваемого участка и обратно пропорциональны его диаметру. Кроме того, в (6.6) входит безразмерный коэффициент 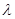 - так называемый коэффициент гидравлического трения (коэффициент Дарси).
- так называемый коэффициент гидравлического трения (коэффициент Дарси).
На основании приведенных выше рассуждений о механизме гидравлического сопротивления трения по длине трубопровода следует отметить, что коэффициент гидравлического трения  зависит от числа Рейнольдса Re и шероховатости стенок
зависит от числа Рейнольдса Re и шероховатости стенок  , т.е.
, т.е.  =f(Re,
=f(Re,  /d). Влияние указанных факторов на величину коэффициента
/d). Влияние указанных факторов на величину коэффициента  при ламинарном и турбулентном режимах движения проявляется по разному. При этом при определении
при ламинарном и турбулентном режимах движения проявляется по разному. При этом при определении  учитывается не абсолютная высота выступов шероховатости, а ее отношение к диаметру трубопровода, т.е. относительная шероховатость
учитывается не абсолютная высота выступов шероховатости, а ее отношение к диаметру трубопровода, т.е. относительная шероховатость  /d. Это вызвано тем, что одна и та же абсолютная шероховатость в трубопроводах разных диаметров оказывает большее влияние на сопротивление движению в случае меньшего диаметра.
/d. Это вызвано тем, что одна и та же абсолютная шероховатость в трубопроводах разных диаметров оказывает большее влияние на сопротивление движению в случае меньшего диаметра.
Первые опыты с целью выявления характера зависимости  от Re и
от Re и  /d были проведены в 1933 г. И. Никурадзе в гладких латунных трубопроводах и трубопроводах с искусственной равномерно-зернистой шероховатостью из кварцевого песка. Песок с различной высотой выступов шероховатости
/d были проведены в 1933 г. И. Никурадзе в гладких латунных трубопроводах и трубопроводах с искусственной равномерно-зернистой шероховатостью из кварцевого песка. Песок с различной высотой выступов шероховатости  наносился сплошным слоем на внутреннюю поверхность трубопроводов разного диаметра. При этом были получены различные значения относительной шероховатости (от
наносился сплошным слоем на внутреннюю поверхность трубопроводов разного диаметра. При этом были получены различные значения относительной шероховатости (от  /d=0,00197 до
/d=0,00197 до  /d=0,066). В изготовленных таким образом трубопроводах при разных расходах измеряли потерю напора и вычисляли коэффициент
/d=0,066). В изготовленных таким образом трубопроводах при разных расходах измеряли потерю напора и вычисляли коэффициент  по формуле Дарси-Вейсбаха.
по формуле Дарси-Вейсбаха.
На рис. 6.3 в логарифмических координатах представлены результаты указанных опытов (график И. Никурадзе), отражающие весьма сложную механику течения жидкости даже в таком простом случае, как равномерное движение в круглых трубопроводах.
На графике И. Никурадзе можно выделить пять характерных зон течения (рис. 6.3).
I зона - зона ламинарного течения (вязкостного сопротивления). В этой зоне весь поток сплошь является ламинарным. Выступы шероховатости плавно обтекаются потоком, и поэтому их высота не оказывает заметного влияния на коэффициент  . В I зоне
. В I зоне  =f(Re) , причем эта функция устанавливается теоретически и имеет вид
=f(Re) , причем эта функция устанавливается теоретически и имеет вид
 (6.7)
(6.7)
Потери напора hl в этой зоне пропорциональны скорости течения в первой степени. I зона существует приблизительно до чисел Re = 2320.
II зона – переходная зона. Эта зона небольшая и находится в пределах 2320< Re<4470. В ней  =f(Re).
=f(Re).
III зона – зона гидравлически гладких труб. При числах 4470<Re<20  в центральной части потока течение турбулентное, а
в центральной части потока течение турбулентное, а 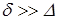 . Поэтому выступы не оказывают влияния на сопротивление, которое определяется по эмпирической формуле Блазиуса для технически гладких труб
. Поэтому выступы не оказывают влияния на сопротивление, которое определяется по эмпирической формуле Блазиуса для технически гладких труб
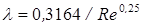 (6.8)
(6.8)
К технически гладким трубам относятся стеклянные, цельнотянутые из цветных металлов, высококачественные стальные трубы, трубы из различных полимеров.
Для расчета  в этой области применяются также формулы Ф.А. Шевелева:
в этой области применяются также формулы Ф.А. Шевелева:
- для гидравлически гладких новых стальных труб
 (6.9)
(6.9)
- для гидравлически гладких новых чугунных труб
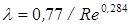 (6.10)
(6.10)
Потери напора в этой зоне пропорциональны  в степени 1,75.
в степени 1,75.
IY зона - зона неполной шероховатости (рис. 6.3). С увеличением числа Re скорость у стенок возрастает, и влияние вязкости уменьшается. При обтекании турбулентным потоком выступов (  ), вышедших из вязкого слоя, за ними появляются завихрения, увеличивающие инерционную составляющую сопротивления. Чем больше
), вышедших из вязкого слоя, за ними появляются завихрения, увеличивающие инерционную составляющую сопротивления. Чем больше  /d трубы, тем раньше, т.е. при меньших значениях Re, наступают эти явления.
/d трубы, тем раньше, т.е. при меньших значениях Re, наступают эти явления.
В этой зоне коэффициент  зависит от Re и от
зависит от Re и от  /d и определяется по эмпирической формуле А.Д. Альтшуля
/d и определяется по эмпирической формуле А.Д. Альтшуля
 (6.11)
(6.11)
Для расчета  в этой зоне применяется также формула Кольбрука-Уайта
в этой зоне применяется также формула Кольбрука-Уайта
 (6.12)
(6.12)
Зона находится в пределах 20  < Re < 500
< Re < 500  . В ней потери напора пропорциональны
. В ней потери напора пропорциональны  в степени 1,75¸2.
в степени 1,75¸2.
Y зона - зона гидравлически шероховатых труб или квадратичного сопротивления. При увеличении числа Re до значений, больших 500  , скорости у стенки возрастают настолько, что непосредственное влияние вязкости становится весьма малым. Условно принимают, что толщина вязкого слоя при этом равна нулю.
, скорости у стенки возрастают настолько, что непосредственное влияние вязкости становится весьма малым. Условно принимают, что толщина вязкого слоя при этом равна нулю.
В этой зоне коэффициент  не зависит от числа Re и определяется по эмпирической формуле И. Никурадзе
не зависит от числа Re и определяется по эмпирической формуле И. Никурадзе
 (6.13)
(6.13)
или по более простой формуле Шифринсона
 (6.14)
(6.14)
Потери напора в V зоне пропорциональны квадрату средней скорости, поэтому эта зона и называется квадратичной. В этой зоне зависимость  =
=  (Re) представлена прямыми, параллельными оси чисел Re и отличающимися друг от друга параметром
(Re) представлена прямыми, параллельными оси чисел Re и отличающимися друг от друга параметром  /d относительной шероховатости (рис. 6.3).
/d относительной шероховатости (рис. 6.3).
Чтобы применить приведенные выше зависимости, справедливые для песочной шероховатости, к расчету труб с естественной шероховатостью вводится понятие эквивалентной шероховатости.
Эквивалентная шероховатость для данного трубопровода определяется экспериментальным путем: по опыту устанавливается зависимость  =f(Re); находится значение
=f(Re); находится значение  в квадратичной зоне сопротивления и потом, например, из формулы Шифринсона определяется эквивалентная шероховатость
в квадратичной зоне сопротивления и потом, например, из формулы Шифринсона определяется эквивалентная шероховатость
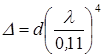 (6.15)
(6.15)
Для труб из различных материалов, условий эксплуатации и т.д. значения эквивалентной шероховатости найдены опытным путем и приводятся в справочной литературе.
Цель работы - опытным путем определить коэффициент гидравлического трения (коэффициент Дарси) трубопровода постоянного сечения при разных числах Рейнольдса и сравнить с результатами расчета по формулам для соответствующей зоны сопротивления.
Описание установки
Экспериментальная установка (рис. 6.4) состоит из емкости 1, центробежного насоса 2 и трубопровода 3 постоянного сечения. Трубопровод 3 состоит из участка 4 без местных сопротивлений, змеевика 5 и участка 6 с внезапным расширением потока. На трубопроводе 3 установлены вентили ВЗ1, ВЗ2, ВЗ3 и ВЗ4 (рис. 6.4).
Центробежный насос 2 всасывает воду из емкости 1 и подает ее в трубопровод 3. Пройдя через все участки трубопровода 3, вода возвращается в емкость 1.
В качестве контрольно-измерительных приборов установлены: манометры P1, P2, P3 и P4, дифференциальный манометр (ДМ) 7, вакуумметр Pвак, турбинный расходомер 8 и термометр 9.
Проведение опытов и измерения
1. Из водопроводной сети наполняется водой емкость 1. Проверяются вентили ВЗ1, ВЗ2, ВЗ3 и ВЗ4. Вентили ВЗ1, ВЗ2 и ВЗ3 должны быть полностью закрыты, вентиль ВЗ4 – полностью открыт.
2. Включается центробежный насос 2 и полностью открывается вентиль ВЗ1.
3. Термометром 9, установленным на емкости 1 измеряется температура воды.
4. Снимаются показания манометров P1 и P2.

| |
| |

Рис. 6.4. Схема экспериментальной установки для
определения потерь напора
5. С помощью расходомера 8 определяется расход воды Q. Цена деления расходомера 1×10-3 м3. Измерение одного расхода проводится в течение 60 с.
6. Каждый опыт проводится при Q=const. Изменение расхода осуществляется закрытием или открытием вентиля ВЗ1.
7. Все измерения проводятся для 5-8 различных расходов воды, а полученные данные заносятся в соответствующие графы табл. 6.1.
Вычисления и составление отчета
1. Определяется по справочным данным (приложение 2) кинематический коэффициент вязкости воды ν по замеренной температуре.
2. Вычисляется объемный расход воды
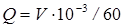 , м3/с (6.16)
, м3/с (6.16)
3. Определяется средняя скорость воды в трубопроводе
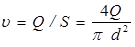 , м/с (6.17)
, м/с (6.17)
4. Вычисляются потери напора по длине опытного участка 4 трубопровода 3. Из уравнения Д. Бернулли, записанного для сечений 1 и 2 (рис. 6.4) трубопровода с постоянным диаметром (u1=u2), имеем
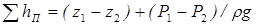 , м (6.18)
, м (6.18)
где P1 и P2 – показания манометров, Па
Для рассматриваемого участка 4 трубопровода 3 z1=0; z2=0,33 м, а также пренебрегая потерями напора в плавном повороте зависимость (6.18) принимает вид
 , м (6.19)
, м (6.19)
5. По формуле Дарси-Вейсбаха (6.6) для каждого опыта определяется экспериментальное значение коэффициента гидравлического трения λопт.
 (6.20)
(6.20)
6. Вычисляется число Рейнольдса и по его значению определяется режим движения жидкости в трубопроводе, а, следовательно, область сопротивления
 (6.21)
(6.21)
7. В зависимости от режима движения и области гидравлического сопротивления по соответствующим формулам (6.7), (6.8), (6.11), (6.13) и (6.14) вычисляются теоретические значения коэффициента гидравлического трения λт. Полученные значения λт сравниваются с опытными λопт и определяется ошибка по формуле
 (6.22)
(6.22)
Результаты вычислений заносятся в табл. 6.1.
8. Строятся графики опытной и теоретической зависимости для коэффициента гидравлического трения, на которых отмечаются характерные зоны гидравлического сопротивления.
Таблица 6.1.
| № опыта | Температура воды t, оС | Кинематическая вязкость воды ν, м2/с | Показания манометров | Потери напора hl, м | Средняя скорость u, м/с | Число Рейнольдса (область сопротивления) Re | Коэффициент гидравлического трения λ | Отклонение (ошибка) e, % | |||
| P1, Па | P2, Па | ||||||||||
| опытный λопт | вычис-ленный λт | ||||||||||
| 1. | |||||||||||
| 2. | |||||||||||
| 3. | |||||||||||
| 4. | |||||||||||
| 5. | |||||||||||
| 6. | |||||||||||
| 7. | |||||||||||
| 8. |
Примечания: длина экспериментального участка трубопровода l = 10 м; диаметр трубопровода d = 15 мм
В выводах по работе необходимо охарактеризовать влияние на коэффициент гидравлического трения пограничной геометрии и числа Рейнольдса.
Лабораторная работа № 7
Дата добавления: 2015-04-18; просмотров: 326; Мы поможем в написании вашей работы!; Нарушение авторских прав |