
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ
Основы теории и цель работы
Местными гидравлическими сопротивлениями называются технические устройства, которые устанавливаются на трубопроводах или каналах и вызывают изменение площади или ориентации живого сечения потока. К ним относятся: запорно-регулирующая арматура (краны, вентили, задвижки), регулирующие клапаны, соединение трубопроводов разных диаметров (диффузоры, конфузоры, внезапное расширение, внезапное сужение), диафрагмы, повороты труб (отводы, колена) и другие.
В зависимости от факторов, вызывающих потери напора, в местных сопротивлениях различают потери трения и вихревые потери.
Потери на трение вызываются торможением потока стенками, которое приводит к неравномерному распределению скоростей по сечениям потока и к появлению напряжений трения между смещающимися струйками жидкости. Местные деформации потока сопровождаются увеличением неравномерности скоростей в его сечениях, вызывающим возрастание местных потерь трения.
Вихревые потери связаны с отрывами потока от стенок, происходящи-ми при резких изменениях конфигурации каналов. Возникающие при этом интенсивные вихреобразования приводят к сильному возрастанию местной потери напора.
Рассмотрим структуру потока при его отрыве от твердой стенки (рис. 7.1). В этом случае транзитный поток отделяется от циркуляционной зоны некоторой воображаемой поверхностью раздела.
Выделим часть этой поверхности А-А с прилегающими к ней струйками транзитного потока и потока циркуляционной зоны (рис. 7.2, а). Отметим, что в любом поперечном сечении скорости транзитного потока больше скоростей потока в циркуляционной зоне.
Пусть по какой-либо случайной причине произошло искривление поверхности раздела (рис. 7.2, б). При этом возникают поперечные инерционные силы, действующие в сторону увеличения кривизны. Таким образом, возникающее искривление поверхности раздела начинает затем прогрессировать, и она вследствие разницы скоростей в прилегающих струйках будет сворачиваться в отдельные вихри и распадаться (рис. 7.2, в, г). Затем поверхность раздела возникает опять, и весь процесс повторяется сначала, т.е. данный процесс носит автоколебательный характер.
Итак, поверхность раздела является неустойчивой, и при своем распаде она генерирует в потоке вихри.
Рассмотрим поведение вихря, образовавшегося при распаде поверхности раздела и попавшего в транзитный поток. Результирующая скорость в точке 1 вихря будет, очевидно, больше скорости в точке 2 (рис. 7.1). Давление же, напротив, будет согласно уравнению Д. Бернулли больше в точке 2. Итак, на вращающийся в поступательном потоке вихрь действует поперечная сила, выталкивающая его в транзитный поток. В транзитном потоке первичные вихри (макро-вихри), образовавшиеся при распаде поверхности раздела, постепенно распадаются на вихри меньшего размера, те, в свою очередь, на еще более мелкие вихри и т.д. Этот процесс идет до тех пор, пока они не достигнут размера диссипативных вихрей.
Кинетическая энергия, захваченная у потока макровихрями при их образовании, передается ими почти без потерь диссипативным вихрям. А они растрачивают ее на работу против сил вязкости. Эта энергия превращается в тепловую, и рассеивается.
Рассмотренная схема явлений при отрыве относится к случаю турбулентного потока, чаще всего встречающемуся на местных сопротивлениях.
Остановимся теперь на способах определения потерь энергии при протекании жидкости через местные сопротивления.
Пусть имеется на горизонтальном трубопроводе некоторое местное сопротивление (рис. 7.3). Его влияние на поток начинает обнаруживаться в некотором сечении 1-1, расположенном перед сопротивлением. Это влияние выражается в отклонении пьезометрической линии от прямой, характерной для равномерного движения жидкости в трубе до сечения 1-1.
Пройдя через местное сопротивление, поток на некоторой длине постепенно восстанавливает признаки равномерного движения и, начиная с некоторого сечения 2-2, вновь становится равномерным.
Таким образом, участок местного сопротивления располагается между сечениями 1-1 и 2-2 (рис. 7.3). Вся потеря напора на этом участке относится к местной потере. Однако для удобства расчетов и чтобы выделить влияние местного сопротивления, принято к местной потере относить лишь дополнительную потерю, которая возникает в трубопроводе с местным сопротивлением по сравнению с тем же трубопроводом без местного сопротивления, т.е
.
 , (7.1)
, (7.1)
где hn – потеря напора в трубопроводе с местным сопротивлением, м; hl – потеря напора по длине того же трубопровода без местного сопротивления, м.
Данный подход лежит в основе методики экспериментального определения коэффициентов местных сопротивлений.
В инженерной практике для расчета местных потерь напора применяется формула Вейсбаха, выражающая потери в долях от скоростного напора

Рис. 7.1. Структура потока при отрыве от твердой стенки

Рис. 7.2. Схема генерирования вихрей в потоке
|
|
|
|
|
|

Рис. 7.3. Пьезометрическая линия для горизонтального трубопровода
с местным сопротивлением
 , (7.2)
, (7.2)
где ζм – безразмерный коэффициент местного сопротивления; u – средняя скорость в сечении трубопровода перед местным сопротивлением или после него.
В общем случае, согласно теории подобия, коэффициенты местных гидравлических сопротивлений зависят от пограничной геометрии и режима движения, характеризуемого числом Re.
При малых числах Рейнольдса жидкость движется через местные сопротивления без отрыва. Следовательно, потери напора обусловливаются непосредственным действием сил вязкого трения и пропорциональны скорости потока в первой степени. Коэффициенты местного сопротивления в этом случае связаны с числом Рейнольдса зависимостью
 , (7.3)
, (7.3)
где A – коэффициент, зависящий от вида местного сопротивления и степени стеснения потока.
С увеличением числа Рейнольдса наряду с потерями на трение возникают потери напора, обусловленные отрывом потока и образованием вихрей (переходная область сопротивления). При больших числах Рейнольдса вихреобразование приобретает основное значение, потери напора становятся пропорциональны квадрату скорости, так как коэффициент ζм перестает зависеть от Re и определяется только геометрией потока (так называемая квадратичная или автомодельная область сопротивления).
Учитывая, что условия движения жидкости через местные сопротивления (резкое изменение сечений и направления течения) способствуют возникновению турбулентности при значительно более низких числах Re, чем при движении в трубопроводах постоянного сечения, они часто работают в условиях автомодельности по Re.
Для определения коэффициентов местных сопротивлений А.Д. Альтшулем рекомендуется следующая формула
 , (7.4)
, (7.4)
где  - коэффициент соответствующего местного сопротивления в области квадратичного сопротивления.
- коэффициент соответствующего местного сопротивления в области квадратичного сопротивления.
Для некоторых видов местных сопротивлений значения коэффициентов А и  приведены в табл. 7.1.
приведены в табл. 7.1.
В отдельных случаях для определения hм получены теоретические решения.
Таблица 7.1
Значения коэффициентов А и  для некоторых видов местных
для некоторых видов местных
сопротивлений
| Виды местных сопротивлений | А | 
| Виды местных сопротивлений | А | 
|
| Вентиль обыкновенный Угловой вентиль Шаровой клапан Угольник 900 Колено 900 Тройник | 0,8 1,4 0,2 0,3 | Задвижка: полное открытие n=1 n=0,5 Диафрагма: n=0,64 n=0,16 | 0,15 |
.
 При внезапном расширении потока в трубопроводе от площади S1 до S2 (рис. 7.4), жидкость не растекается по контуру излома стенок, а следует по более плавным линиям тока. Около стенок образуется пространство, в котором жидкость находится во вращательном движении.
При внезапном расширении потока в трубопроводе от площади S1 до S2 (рис. 7.4), жидкость не растекается по контуру излома стенок, а следует по более плавным линиям тока. Около стенок образуется пространство, в котором жидкость находится во вращательном движении.
Потеря напора, происходящая при внезапном расширении потока реальной жидкости, находится с помощью уравнения Д. Бернулли, записанного для сечений 1-1 и 2-2, где движение считается плавно изменяющимся. Тогда
 (7.5)
(7.5)
Применяя теорему о количестве движения и произведя необходимые преобразования, выражаем hв.р через средние скорости
 (7.6)
(7.6)
Называя разность (u1 – u2) потерянной скоростью следует, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости (теорема Борда). Зависимость (7.6) записывается в виде
 или
или  (7.7)
(7.7)
С учетом того, что по уравнению неразрывности u1s1=u2s2, из (7.7) получим
 , (7.8)
, (7.8)
где  ;
; 
 При внезапном сужении потока (рис. 7.5), так же как и при внезапном расширении, создаются пространства с вальцами вращающейся жидкости. Коэффициент внезапного сужения ζв.с зависит от соотношения площадей живого сечения S1 (большее сечение) и S2 (меньшее сечение). Средние величины коэффициента ζв.с приведены в табл. 7.2.
При внезапном сужении потока (рис. 7.5), так же как и при внезапном расширении, создаются пространства с вальцами вращающейся жидкости. Коэффициент внезапного сужения ζв.с зависит от соотношения площадей живого сечения S1 (большее сечение) и S2 (меньшее сечение). Средние величины коэффициента ζв.с приведены в табл. 7.2.
Таблица 7.2
| S2/S1 | 0,01 | 0,10 | 0,20 | 0,40 | 0,60 | 0,80 | 1,0 |
| ζв.с | 0,50 | 0,45 | 0,40 | 0,30 | 0,22 | 0,12 |
Коэффициент потерь напора при постепенном расширении потока (расширяющиеся переходные конусы или диффузоры) определяется по формуле
 , (7.9)
, (7.9)
где S2 и S1 – площади живого сечения за расширением и до него, а коэффициент k, находится по табл. 7.3 в зависимости от центрального угла (угла конусности) q.
Таблица 7.3
| q 0 | ||||||||||||
| k | 0,13 | 0,17 | 0,26 | 0,41 | 0,71 | 0,90 | 1,03 | 1,12 | 1,10 | 1,06 | 1,05 | 1,02 |
Коэффициент потерь напора при постепенном сужении потока (конфузоре) находится по зависимости
 , (7.10)
, (7.10)
где n - отношение площадей живого сечения до конфузора и за ним; 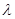 -коэффициент Дарси при движении жидкости в трубопроводе;
-коэффициент Дарси при движении жидкости в трубопроводе; 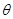 - угол конусности.
- угол конусности.
Для измерения расхода жидкости в трубопроводах применяются диафрагмы, представляющие собой установленные перпендикулярно к направлению течения тонкий диск с круглым отверстием площадью S0 в центре. Коэффициент сопротивления диафрагмы (  ), установленной в трубопроводе постоянного сечения, зависит от отношения площади отверстия S0 к площади живого сечения трубы S и принимается по табл. 7.4.
), установленной в трубопроводе постоянного сечения, зависит от отношения площади отверстия S0 к площади живого сечения трубы S и принимается по табл. 7.4.
Таблица 7.4
| S0/S | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |

| 47,8 | 17,5 | 7,8 | 3,75 | 1,80 | 0,80 | 0,29 | 0,06 | |||

Коэффициент потерь напора для колена с закруглением  зависит от угла
зависит от угла  и отношения радиуса трубопровода r0 к радиусу поворота Rзакр (рис. 7.6.). Если угол поворота
и отношения радиуса трубопровода r0 к радиусу поворота Rзакр (рис. 7.6.). Если угол поворота  не равен 900, следует приведенные в табл. 7.5 данные ζзакр умножить на отношение α/900.
не равен 900, следует приведенные в табл. 7.5 данные ζзакр умножить на отношение α/900.
Таблица 7.5
| r0/Rзакр | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| ζзакр | 0,131 | 0,138 | 0,158 | 0,206 | 0,294 | 0,440 | 0,661 | 0,977 | 1,408 | 1,978 |
Для простой задвижки, перекрывающей трубопровод круглого поперечного сечения, коэффициент потерь напора ζз зависит от степени закрытия  задвижки, которая характеризуется отношением a/d (рис. 7.7). В табл.7.6 приведены значения ζз в зависимости от a/d.
задвижки, которая характеризуется отношением a/d (рис. 7.7). В табл.7.6 приведены значения ζз в зависимости от a/d.
Таблица 7.6
| a/d | 1/4 | 3/8 | 1/2 | 5/8 | 3/4 | 7/8 |
| ζз | 0,26 | 0,81 | 2,06 | 5,52 | 17,0 | 97,8 |
Таким образом, следует отметить, что коэффициенты местных гидравлических сопротивлений находятся, как правило, опытным путем и некоторые из них приведены выше.
В действительных условиях производственного объекта расстояния между отдельными местными сопротивлениями могут оказаться незначительными. В этом случае возможно взаимное влияние местных сопротивлений друг на друга, и их коэффициенты сопротивлений существенно отличаются от табличных.
В ряде случаев при расчете трубопровода местные потери напора выражают в виде эквивалентной длины lэ прямого участка, сопротивление трения которого равно рассматриваемым местным потерям напора, т.е. из условия
 или
или  (7.11)
(7.11)
Поскольку коэффициенты  и
и  в общем случае являются функциями пограничной геометрии и числа Re, то lэ для данного местного сопротивления и трубопровода будет постоянна лишь в области автомодельности.
в общем случае являются функциями пограничной геометрии и числа Re, то lэ для данного местного сопротивления и трубопровода будет постоянна лишь в области автомодельности.
Цель работы- опытным путем определить коэффициент местного гидравлического сопротивления змеевика и сравнить его с литературными данными.
Описание установки
Данную лабораторную работу выполняют на той же установке, что и работу № 6. В работе опытным путем находятся потери напора и коэффициенты местного сопротивления змеевика 5 (рис. 6.4). Для измерения потерь напора в змеевике 5 служат манометры Р2 и Р3.
Проведение опытов и измерения
1. Из водопроводной сети наполняется водой емкость 1. При этом вентиль ВЗ1 полностью закрывается, а ВЗ4 – открывается (рис. 6.4).
2. Включается центробежный насос 2 и открывается вентиль ВЗ1.
3. Измеряется температура воды термометром 9.
4. Снимаются показания манометров Р2 и Р3.
5. Определяется расход воды по расходомеру 8.
6. Измерения проводятся для 7-10 опытов, в каждом из которых расход воды регулируется с помощью вентиля ВЗ1. Каждый опыт проводится при Q=const.
Все измеренные величины заносятся в табл. 7.7.
Вычисления и составление отчета
1. По замеренному объемному расходу Q определяются в каждом опыте средние скорости движения воды в змеевике.
2. Записывается уравнение Д. Бернулли для сечений 2 и 3 относительно плоскости сравнения 0-0 (рис.7.8)
|
|

Рис.7.8. Змеевик
 , (7.12)
, (7.12)
где z2 = 0; z3 = h = 1,3 м; Р2 и Р3 - показания манометров;  , т.к. d = const.
, т.к. d = const.
Из уравнения (7.12) определяются суммарные потери напора
 , м (7.13)
, м (7.13)
Суммарные потери напора складываются из потерь напора по длине и суммы местных потерь, т.е.
 , м (7.14)
, м (7.14)
где hl - потери напора по длине получаем, используя данные лабораторной работы № 6, тем более, что длина змеевика от сечения 2 до сечения 3 равна 10 м.
Из (7.14) находится сумма местных потерь напора
 , м (7.15)
, м (7.15)
Потери напора в змеевике определяются по формуле Вейсбаха
 , м (7.16)
, м (7.16)
где  - коэффициент местного гидравлического сопротивления змеевика;
- коэффициент местного гидравлического сопротивления змеевика;  - коэффициент сопротивления петли змеевика; n - количество петель змеевика (n=4).
- коэффициент сопротивления петли змеевика; n - количество петель змеевика (n=4).
Приравнивая (7.15) и (7.16) находится зависимость для определения опытного значения коэффициента местного гидравлического сопротивления петли змеевика
 , (7.17)
, (7.17)
Эквивалентная длина змеевика определяется по формуле (7.11)
 , м (7.18)
, м (7.18)
Теоретическое значение коэффициента местного гидравлического сопротивления змеевика сводится к определению коэффициентов сопротивления на повороте. В данной работе каждая петля змеевика состоит из двух поворотов на 900. Коэффициент сопротивления одного поворота на 900 рассчитывается по формуле
 , (7.19)
, (7.19)
где d и Rзакр - соответственно диаметр трубы и радиус закругления (рис. 7.6), м.
С учетом (7.19) теоретические значения коэффициентов местного гидравлического сопротивления петли змеевика и змеевика находятся по зависимостям
 ;
;  (7.20)
(7.20)
3. Определяется относительная погрешность между опытными и теоретическими данными коэффициентов гидравлического сопротивления змеевика
 (7.21)
(7.21)
Результаты наблюдений и вычислений заносятся в табл. 7.7.
| Вид местного сопротивления |
Средние скорости
 ,
м/с ,
м/с
| Потери напора по длине hl 2-3,м |
Местные потери напора
 ,м ,м
| Коэффициенты местных потерь | |
| Опытные | Вычисленные или справочные | ||||
| Петля змеевика Змеевик |
Таблица 7.7
В выводе по работе необходимо пояснить причины местных потерь напора в змеевике.
Лабораторная работа № 8
Дата добавления: 2015-04-18; просмотров: 1110; Мы поможем в написании вашей работы!; Нарушение авторских прав |