Лекция 13. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ

1. Барометрическая формула

Хаотические молекулярные движения

приводят к тому, что частицы газа равномерно распределяются по объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число частиц. В равновесном состоянии давление и температура газа также одинаковы во всем объеме. Но так обстоит дело только в том случае, когда на молекулы не действуют внешние силы. При наличии же таких сил молекулярные движения приводят к своеобразному поведению газов.

Возьмем, например, газ (воздух), находящийся под действием силы тяжести. Если бы отсутствовало тепловое движение молекул, то все они под действием силы тяжести "упали" бы на Землю. Если бы отсутствовала сила тяжести, молекулы разлетелись бы по всему пространству.

Рассмотрим вертикальный столб воздуха (рис. 13.1). Пусть у поверхности Земли (х = 0) давление равно Р_о, а на высоте х равно Р. При

Если же считать, что температура на всех высотах одна и та же (что, вообще говоря, неверно), то, интегрируя (13.3), находим

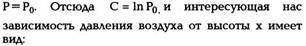
где С - постоянная интегрирования, которая находится из условия, что при х = 0 давление

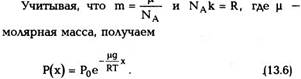
Уравнение (13.6) называется барометрической формулой.Из этого уравнения видно, что давление газа убывает с высотой по экспоненциальному закону.

Так как давление газа P = nkT, то из (13.6) вытекает, что концентрация молекул на высоте х

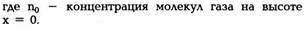
изменении высоты на dx давление уменьшается на dP. Изменение же давление dP равно разности весов воздуха над единичной площадкой на высотах х и х 4- dx, то есть

где р — плотность воздуха, g — ускорение силы тяжести.

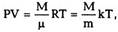
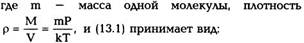
Из уравнения состояния

Разделяя в (13.2) переменные Р и х, получим: