Понятие о вероятности

К понятию вероятности, в отличие от "достоверности", мы прибегаем в тех случаях, когда речь идет о случайных событиях, то есть таких, условия наступления которых по тем или иным причинам неизвестны и которые поэтому нельзя с уверенностью предсказать.

Например, бросая много раз монету, мы можем быть уверены, что приблизительно в половине случаев она упадет обращенной вверх стороной с гербом. Поэтому говорят, что вероятность выпадения герба равна 1/2. И это

будет тем вероятней, чем больше будет число бросаний.

Эти и подобные им опыты позволяют нам дать
следующее определение вероятности:

вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего.

Если из N опытов N' приводят к реализации интересующего нас события, то вероятность w этого события

Рассмотрим теперь еще один пример, который позволит нам осуществить одно из важных положений теории вероятностей и, кроме того, дать еще одно определение самой величины вероятности.

Пусть в ящике лежат 20 абсолютно одинаковых шаров, 5 из которых окрашены в белый цвет, а остальные — в черный. Извлечем из ящика один шар. Спрашивается, какова вероятность того, что будет вынут белый шар? Так как для каждого шара (белого или черного) вероятность быть вынутым равна 1/20, а всего белых шаров пять (и нам все равно, какой из них будет вынут), то искомая вероятность равна сумме вероятностей для всех белых шаров:

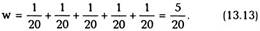
Этот результат выражает одно из важных положений теории вероятностей — теорему сложения вероятностей,которая гласит: если w,_r w₂, w₃ и т.д. — вероятности нескольких исключающих друг друга событий, то вероятность того, что осуществится или событие 1, или2, или3 и т.д., равна сумме вероятностей всех этих событий:

Приведенный пример позволяется нам дать новое определение вероятности, несколько отличающееся от прежнего: вероятность данного события равна отношению числа случаев, благоприятствующих его наступлению, к общему числу возможных случаев, если все случаи равновозможны. В нашем примере с шарами число случаев, благоприятствующих наступлению события равно 5, а общее число возможных случаев - 20.

Из этого определения вероятности ясно, что вероятность достоверного события равна единице, или

газа в элементе объема dV = dxdydz вблизи

точки с координатами (x,y,z), при этом молекула обладает потенциальной энергией U(x,y,z).

Нам остается изложить еще одно важное положение теории вероятностей — теорему умножения вероятностей.Эта теорема гласит: если имеются несколько независимых событий, вероятности которых w₁₍ w₂, w₃,..., то вероятность того, что наступит одновременно событие 1 исобытие 2, исобытие 3 и т.д., равна произведению вероятностей каждого из них, т.е.