
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
И, наконец,
наиболее вероятной скорости vHB. Начнем со средней арифметической скорости (v). На основании (13.20)

трактовать, как вероятность нахождения молекулы в элементарном объеме пространства скоростей dvx,dvy,dvz вблизи точки с координатами
(vx,vy,vz).
Формула (13.25) называется распределением Максвелла по компонентам скоростей.
Если нас интересует вероятность того, что молекула газа обладает абсолютной скоростью поступательного движения в пределах от v до v+dv, то вместо dvx,dvy,dvz мы должны взять
объем, заключенный в пространстве скоростей между сферой радиусом v+ dv и сферой радиусом v, который равен 4?rv2dv. Тогда вероятность того, что молекула обладает при тепловом равновесии абсолютной скоростью от v до v+dv, дается выражением


|

|
После несложного интегрирования по частям получим окончательно:
газовая постоянная.
Для определения среднеквадратичной скорости находим

Стоящий в (13.30) интеграл является частным случаем так называемого интеграла Пуассона, который имеет вид

где dNv — число таких молекул. Эта формула
где а — положительная постоянная. Он равен:

|

|

|
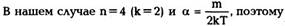
|

|

|

|

|
Дата добавления: 2014-10-31; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |