
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения Максвелла для электромагнитного поля
Теория Максвелла представляет собой феноменологическую теорию электромагнитного поля. В ней не рассматриваются молекулярное строение среды и внутренние механизмы процессов, происходящих в среде в электромагнитном поле. Электрические и магнитные свойства среды характеризуются тремя величинами: диэлектрической проницаемостью e, магнитной проницаемостью m и удельной электрической проводимостью s. Предполагается, что эти параметры среды известны из опыта.
Теория Максвелла – макроскопическая теория. В ней рассматриваются макроскопические поля макроскопических зарядов и токов, т. е. таких систем покоящихся и движущихся зарядов, пространственная протяженность которых намного больше размеров атомов и молекул.
В основе теории лежат четыре уравнения, которые могут быть представлены в двух формах: интегральной и дифференциальной.
Первое уравнение Максвелла является обобщением закона электромагнитной индукции. Оно имеет следующий вид
 . (14.4.1.)
. (14.4.1.)
Это уравнение означает, что циркуляция напряженности E электрического поля по произвольному замкнутому контуру L , мысленно проведенному в электромагнитном поле, равна взятому с обратным знаком потоку вектора  через поверхность S, ограниченную этим контуром. Иными словами с переменным магнитным полем связано индуцированное вихревое электрическое поле. Причем это электрическое поле существует, не зависимо от того, находится в нем проводник или нет.
через поверхность S, ограниченную этим контуром. Иными словами с переменным магнитным полем связано индуцированное вихревое электрическое поле. Причем это электрическое поле существует, не зависимо от того, находится в нем проводник или нет.
Второе уравнение Максвелла
 (14.4.2.)
(14.4.2.)
означает, что циркуляция напряженности H магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна полному току через поверхность S, ограниченную этим контуром. Полный ток равен сумме тока проводимости
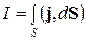
и тока смещения

Из этого уравнения следует, что даже в отсутствие тока электрических зарядов возникает индуцированное магнитное поле, связанное с переменным электрическим полем.
Третье уравнение является обобщением электростатической теоремы Гаусса. Оно имеет вид
 (14.4.3.)
(14.4.3.)
где r – объемная плотность свободных зарядов. Это уравнение означает, что поток электрической индукции (электрического смещения) D через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен суммарному свободному заряду в объеме V, ограниченном этой поверхностью.
Четвертое уравнение
 (14.4.4)
(14.4.4)
означает, что поток магнитной индукции B, через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен нулю.
Дата добавления: 2015-02-09; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |