Гармонические колебания. Колебательным процессом называется процесс, который повторяется через определенный промежуток времени

Колебательным процессом называется процесс, который повторяется через определенный промежуток времени. Колебания весьма разнообразны по своей физической природе, поэтому различают механические, электромагнитные и др. Однако разнообразные по природе, колебания имеют общие закономерности и описываются однотипными математическими методами.

Колебания, которые возникают в системе в результате какого-либо однократного начального отклонения этой системы от состояния устойчивого равновесия, называются свободными колебаниями. В случае свободных колебаний система не подвержена действию переменных внешних сил.

Примером свободных колебаний являются колебания математического пружинного и физического маятников.

Самым простым колебательным процессом является гармоническое колебание материальной точки. Гармоническим колебанием называется колебания, протекающие по гармоническому закону (т.е. по закону синуса или косинуса).Ангармоническими называются колебания, в процессе которого величины, характеризующие колебательное движение не меняются по закону синуса или косинуса.

Гармонические колебания величины x изменяется со временем по закону:

x = A cos (wt+j₀), (15.1.1)

где А – амплитуда колебания (величина равная наибольшему абсолютному значению колеблющейся физической величины x)

Выражение (wt+j₀) определяет значение x в данный момент времени и называется фазой колебания. В момент начала отсчета времени (t=0) фаза равна начальной фазе j₀.

Наименьший промежуток времени, по истечении которого повторяются значения всех величин, характеризующих колебательное движение, называется периодом колебаний (Т). За это время совершается одно полное колебание.

Поскольку синус и косинус периодическая функция с периодом 2p, то значения величины x повторяются, если фаза изменится на величину 2p, т.е. x₁ = x₂;

A sin (wt₁+j) = A sin (wt₂+j),

Разность фаз

d = wt₁-wt₂ = 2p

или

w(t₁-t₂) = 2p.

Но если величина x приобрела прежнее значение, то интервал времени равен периоду колебаний:

t₁-t₂ = T.

Из приведенных соображений следует, что

wT = 2p,

где w - циклическая (круговая) частота.

Циклической частотой периодических колебания называется число полных колебаний, которые совершаются за 2p единиц времени.

Частотой периодических колебаний (n) называют число полных колебаний, которые совершаются за единицу времени. Поэтому соотношения между рассматриваемыми величинами имеют следующий вид:

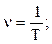
. (15.1.2)

Единицей измерения частоты периодических колебаний является герц (Гц).