
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двухфакторный дисперсионный анализ
Обобщением однофакторного дисперсионного анализа является многофакторный анализ, когда учитывается одновременно несколько факторов. Рассмотрим воздействие на признак  двух независимых факторов
двух независимых факторов  и
и 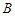 , имеющих
, имеющих  и
и  фиксированных уровней соответственно. Для всех возможных сочетаний уровней проведено одно измерение, т.е. всего измерялось
фиксированных уровней соответственно. Для всех возможных сочетаний уровней проведено одно измерение, т.е. всего измерялось  значений
значений  признака
признака  , где
, где  - индекс уровня фактора
- индекс уровня фактора  ,
,  - индекс уровня фактора
- индекс уровня фактора 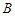 .
.
Результаты наблюдений представляют в виде таблицы 2.6.
Т а б л и ц а 2.6
Матрица экспериментов
Уровень фактора 
| Уровни фактора 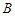
| |||

| 
| … | 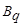
| |

| 
| 
| … | 
|
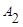
| 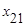
| 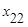
| … | 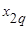
|
| … | … | … | … | … |

| 
| 
| … | 
|
Расчетные формулы средних значений признака  :
:
· на каждом уровне фактора 
 . (2.12)
. (2.12)
· на каждом уровне фактора 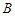
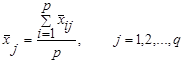 . (2.13)
. (2.13)
· по всем наблюдениям
 . (2.14)
. (2.14)
Расчетные формулы дисперсий признака  :
:
· на каждом уровне фактора 
 . (2.15)
. (2.15)
· на каждом уровне фактора 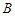
 . (2.16)
. (2.16)
Число степеней свободы:

Суммы, характеризующие влияние факторов на признак  , и общая сумма квадратов:
, и общая сумма квадратов:

 ; (2.17)
; (2.17)
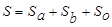 ,
,
где  - остаточная сумма квадратов отклонений. Тогда
- остаточная сумма квадратов отклонений. Тогда
 . (2.18)
. (2.18)
Дисперсии:

Статистическая значимость влияния на признак  факторов проверяется сравнением расчетных значений
факторов проверяется сравнением расчетных значений  - критерия
- критерия
 =
=  /
/  ;
; 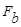 =
=  /
/  (2.19)
(2.19)
с критическими значениями критерия  при заданных значениях
при заданных значениях  и
и  .
.
Если  , то влияние факторов значимо (существенно). В этом случае дисперсионный анализ может быть продолжен проверкой значимости средних значений групп фактора
, то влияние факторов значимо (существенно). В этом случае дисперсионный анализ может быть продолжен проверкой значимости средних значений групп фактора  или фактора
или фактора 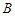 . Для этого достаточно визуально сравнить средние значения и дисперсии признака
. Для этого достаточно визуально сравнить средние значения и дисперсии признака  по столбцам или строкам.
по столбцам или строкам.
Пример 2.2 [1].При спектрографическом исследовании были проведены испытания с целью проверки влияния различных электродов (фактор  ) и фотопластинок (фактор
) и фотопластинок (фактор 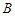 ) на признак, характеризующий интенсивность света. Результаты испытаний и дисперсионного анализа приведены в таблице 2.7, расчетные формулы – в таблице 2.9
) на признак, характеризующий интенсивность света. Результаты испытаний и дисперсионного анализа приведены в таблице 2.7, расчетные формулы – в таблице 2.9
Т а б л и ц а 2.7
Дисперсионный анализ влияния электродов и
фотопластинок

Продолжение таблицы 2.7

Сводка дисперсионного анализа, полученная с помощью инструмента Двухфакторный дисперсионный анализ без повторенийпакета анализа, приведена в таблице 2.8.
Т а б л и ц а 2.8
Сводка дисперсионного анализа

Как следует из дисперсионного анализа для:
· электродов  , т.е. гипотеза о том, что электроды не влияют на исследуемый признак, подтверждается;
, т.е. гипотеза о том, что электроды не влияют на исследуемый признак, подтверждается;
· фотопластинок  , т.е. фотопластинки существенно влияют на исследуемый признак.
, т.е. фотопластинки существенно влияют на исследуемый признак.
Результаты дисперсионного анализа таблиц 2.7 и 2.8 совпадают. Анализ средних значений и дисперсий по столбцам (фактор 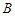 - фотопластинки) показывает, что уровень
- фотопластинки) показывает, что уровень  обеспечивает высокое среднее значение признака и относительно невысокое рассеивание возможных значений признака около среднего значения.
обеспечивает высокое среднее значение признака и относительно невысокое рассеивание возможных значений признака около среднего значения.
Диалоговое окно инструмента Двухфакторный дисперсионный анализ без повторенийпредставлено на рис. 2.2.

Рис. 2.2. Диалоговое окно Двухфакторный
дисперсионный анализ без повторений
Т а б л и ц а 2.9
Расчетные формулы
| Адрес ячейки | Формула | Адрес ячейки | Формула |
| B7 | =СУММ(b3:b6) | C21 | =a21*b21 |
| B8 | =b7/$a$21 | D21 | =a21-1 |
| B9 | =b3-b$8 | E21 | =b21-1 |
| B13 | =b9^2 | F21 | =c21-1 |
| B17 | =СУММ(b13:b16) | G21 | =d21*e21 |
| B18 | =b17/$d$21 | G23 | =СУММ(b23:f23) |
| B22 | =b8-$g$8 | I22 | =a21*g23 |
| B23 | =b22^2 | I23 | =i22/e21 |
| G3 | =СУММ(b3:f3) | H10 | =h3-$h$7 |
| H3 | =g3/$b$21 | I10 | =h10^2 |
| I3 | =b3-$h3 | I14 | =СУММ(i10:i13) |
| N3 | =i3^2 | I15 | =b21*i14 |
| S3 | =СУММ(n3:r3) | I16 | =i15/d21 |
| T3 | =s3/$a$21 | K10 | =b3^2 |
| P10 | =СУММ(k10:o10) | I19 | =h19/g21 |
| P14 | =СУММ(p10:p13) | K22 | =i16/i19 |
| P15 | =p14-c21*h8^2 | L22 | =i23/i19 |
| P16 | =p15/f21 | M22 | =FРАСПОБР(j22;d21;g21) |
| H19 | =p15-i22-i15 | N22 | =FРАСПОБР(j22;e21;g21) |
При изучении совместного действия на результативный признак более двух факторов дисперсионный анализ усложняется. Этот анализ дает возможность оценить не только влияние отдельных факторов, но и влияние взаимодействия между ними.
В выше приведенных расчетах предполагалось, что каждому сочетанию факторов соответствует одно наблюдение. Результаты могут дать большую информацию, если вместо одного измерения провести несколько (два, три) измерений. Повторные испытания можно рассматривать как дополнительный фактор. В этом случае по сравнению с двухфакторным анализом без повторений можно оценить эффект взаимодействия основных факторов  и
и 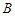 .
.
Пример 2.3[7].Студенты провели факторный эксперимент, в ходе которого измерялось время растворения болеутоляющих таблеток в стакане воды. В эксперименте исследовались два фактора: торговая марка (N1, N2, N3) и температура воды (холодная и теплая). Продолжительность растворения (в секундах) 24 таблеток приведена в таблице 2.10.
Установить существует ли статистически значимый эффект: разновидности таблетки, температуры воды и взаимодействия между разновидностью таблетки и временем ее растворения, если уровень значимости равен 0,05?
Для ответа на эти вопросы выполним дисперсионный анализ с помощью инструмента Двухфакторный дисперсионный анализ с повторениями, диалоговое окно которого приведено на рис. 2.3.
Результаты дисперсионного анализа представлены в таблице 2.11.
Т а б л и ц а 2.10
Результаты эксперимента

Т а б л и ц а 2.11
Сводка дисперсионного анализа


Рис.2.3. Диалоговое окно Двухфакторный
дисперсионный анализ с повторениями
Анализ результатов свидетельствует о том, что при уровне значимости 0,05 статистически значимы эффекты:
· разновидности таблетки (разные фирмы), так как 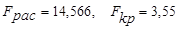 ;
;
· температуры воды -  ;
;
· взаимодействия между разновидностью таблетки и временем ее растворения -  ,
,
причем значительное влияние оказывает температура воды.
Дата добавления: 2015-02-09; просмотров: 366; Мы поможем в написании вашей работы!; Нарушение авторских прав |