Дисперсионный анализ в материаловедении

Определение фактических коэффициентов однородности механических свойств материала – одна из актуальных задач материаловедения, так как:

· его можно рассматривать в виде обобщенного показателя качества производства;

· он позволяет установить влияние на качество продукции свойств исходных материалов и способов изготовления продукции, выявить причины колебания качества и устранить их;

· по ним можно рассчитать фактическую несущую способность конструкций.

Пример 2.3[6].Выполним дисперсионный анализ для определения влияния на прочность бетона в течение месяца недельных режимов работы технологической линии по изготовлению железобетонных изделий. Результаты измерений прочности приведены в таблице 2.12.

Т а б л и ц а 2.12

Результаты измерений прочности бетона

Неделя	Прочность , МПа
		18,5	20,1	20,4	19,7
	18,4	19,8	20,2	20,5
			18,3	19,1	20,3
	20,4	20,5

В данной задаче факторами являются недели, в каждой из которых имеется 5 значений прочности. Следовательно, .

Результаты расчета в среде ЭТ приведены в таблице 2.13.

В таблице 2.14 приведена сводка дисперсионного анализа влияния технологического процесса на прочность бетона, полученная с помощью инструмента Однофакторный дисперсионный анализпакета анализа.

Т а б л и ц а 2.13

Результаты расчета в среде ЭТ

Продолжение таблицы 2.13

Т а б л и ц а 2.14

Дисперсионный анализ влияния технологического

процесса на прочность бетона

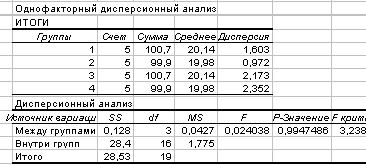
Расчетное значение - критерия Фишера

= / =1,775/0,0426=41,6.

Критическое значение - критерия Фишера при .

Так как , то изменение прочности бетона в течение недельного периода работы технологической линии не случайно и технологический процесс требует регулирования (наладки).

Влияние фактора незначимо, так как остаточная дисперсия значительно больше факторной дисперсии.

В практике строительных материалов дисперсионный анализ применяют для того, чтобы установить оказывает ли существенное влияние некоторый качественный фактор , который имеет уровней на изучаемый результативный признак . Например, если требуется выяснить, какая добавка наиболее эффективна для повышения прочности бетона, то фактор - добавка, а его уровни – количество добавки. Если различие между дисперсиями значимо, то фактор оказывает существенное влияние на признак и в этом случае средние значения на каждом уровне (групповые средние) различаются также значимо.

Пример 2.4[1].Выполним дисперсионный анализ влияния на прочность бетона различного количества добавки.

Результаты измерений прочности приведены в таблице 2.15. Результаты расчета в среде ЭТ представлены в таблице 2.16.

Т а б л и ц а 2.15

Результаты испытаний прочности

Вариант	Прочность , МПа
Без добавки
1-й уровень
2-й уровень
3-й уровень

Т а б л и ц а 2.16

Результаты расчета

Расчетное значение - критерия

= / =702,75/125,458=5,601.

C помощью статистической функции РАСПОБР находим критическое значение - критерия при . . Так как , то влияние добавки на прочность бетона статистически значимо (существенно).

В таблице 2.17 представлена сводка дисперсионного анализа влияния добавки на прочность бетона, полученная с помощью инструмента Однофакторный дисперсионный анализпакета анализа.

Т а б л и ц а 2.17

Дисперсионный анализ влияния добавки

на прочность бетона

Установлено, что добавка влияет на прочность бетона, т.е. средние значения прочности бетона в вариантах в целом существенно различаются между собой и можно перейти к исследованию влияния на прочность различного количества добавки. Для этого надо сравнить средние значения прочности при различных количествах добавки с прочностью бетона без добавки.

Тогда для бетона с добавкой, соответствующей 3-му уровню, расчетное значение - статистики равно

.

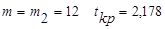Расчетные значения для остальных вариантов приведены в таблицах 2.16-2.17. Критическое значение - статистики при и . Следовательно, 3-й уровень добавки существенно влияет на прочность бетона, а остальные уровни добавки не значимы.

Пример 2.5 [4].Оценить значимость влияний отношения цемент:песок (фактор ) и крупности песка (фактор 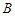) на прочность мелкозернистого бетона для армоцемента по данным эксперимента, приведенным в таблице 2.18.

Т а б л и ц а 2.18

Матрица эксперимента

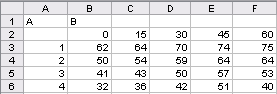
Примечание. Соответствие уровней фактора : 1 - 1:1,6; 2 - 1:2; 3 - 1:2,4; 4 – 1:2,8. Размерность содержания крупных зерен песка, %.

Сводка дисперсионного анализа, полученная с помощью инструмента Двухфакторный дисперсионный анализ без повторений, приведена в таблице 2.19.

Т а б л и ц а 2.19

Дисперсионный анализ влияния факторов

на прочность бетона

Выполним анализ полученных результатов:

· расчетное значение - критерия для фактора 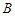- крупность песка - равно 38,54. Критическое значение - критерия равно 3,259, т.е. влияние этого фактора существенно;

· расчетное значение - критерия для фактора , характеризующего отношение Ц:П, равно 188,95. Критическое значение - критерия равно 3,49, т.е. влияние этого фактора существенно (примерно в 5 раз сильнее фактора 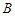- крупность песка);

· первый уровень фактора (Ц:П=1:1,6) обеспечивает получение среднего значения прочности 69 МПа и дисперсию 34 МПа² – это лучшие показатели из всех отношений;

· четвертый уровень фактора 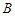(45%) обеспечивает получение среднего значения прочности 61,5 МПа и дисперсию 97,6 МПа² – это лучшие показатели из всех % - х содержаний крупных зерен в песке.

Пример 2.6 [3].Выполнить проверку однородности дисперсий ошибок измерений прочности бетона после пропарки по 10 – ти ежедневным партиям из трех образцов.

Результаты испытаний и расчета в среде ЭТ представлены в таблице 2.20.

Т а б л и ц а 2.20

Результаты расчета в среде ЭТ

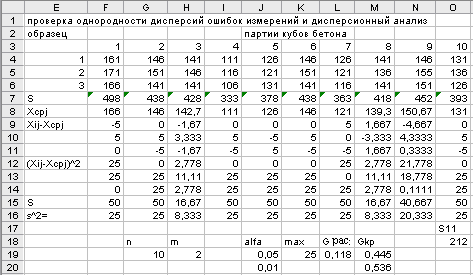
Продолжение таблицы 2.20

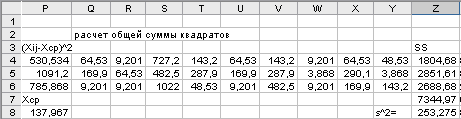
Продолжение таблицы 2.20

Сводка данных дисперсионного анализапредставлена в таблице 2.21.

Т а б л и ц а 2.21

Дисперсионный анализ влияния времени на прочность бетона

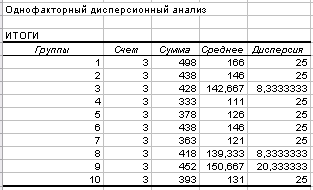
Анализ результатов расчета:

· расчетное значение критерия Кохрена равно =0,118, критическое значение =0,445 при =0,05 и =0,536 при =0,01, т.е. < и отвергать гипотезу об однородности дисперсий ошибок измерений нет причин;

· расчетное значение - критерия равно =36,27, критическое значение =2,393, т.е. > и, следовательно, влияние времени на прочность бетона при постоянных материалах на данном заводе статистически значимо, причем больше ошибки измерения его прочности.

Пример 2.7 [4].Исследовать влияние на коэффициент однородности бетона марки цемента , типа заполнителя , срока испытаний и «периода изготовления» бетона . План эксперимента представлен в таблице 2.22.

Т а б л и ц а 2.22

Матрица эксперимента

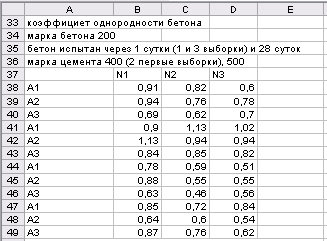
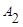В таблице 2.22 заполнители: - гравий речной; - щебень гранитный; - щебень известняковый.

Вначале исследуем влияние на коэффициент однородности бетона типа заполнителя (фактор ) и «периода изготовления» бетона (фактор ). Для этого выполним двухфакторный дисперсионный анализ без повторений первой выборки из таблицы 2.22.

Сводка дисперсионного анализа представлена в таблице 2.23.

Т а б л и ц а 2.23

Дисперсионный анализ влияния типа заполнителя

и «периода изготовления» бетона

Анализ таблицы 2.23 показывает, что расчетные значения - критерия для этих факторов меньше критических значений. Следовательно, тип заполнителя и «период изготовления» не оказывают существенного влияния на коэффициент однородности бетона при испытании образцов через 1 сутки. Аналогичные результаты получены и для второй выборки таблицы 2.22.

Исследуем влияние на коэффициент однородности бетона срока испытаний и марки цемента с помощью инструмента Двухфакторный дисперсионный анализ с повторениямипакета анализа.

Для этого выполним двухфакторный дисперсионный анализ двух выборок, одна из которых содержит первую и вторую выборки таблицы 2.22 (марка цемента 400), вторая – третью и четвертую выборки (марка цемента 500). Сводка дисперсионного анализа представлена в таблицах 2.24 и 2.25.

Т а б л и ц а 2.24

Дисперсионный анализ влияния срока испытаний

Т а б л и ц а 2.25

Дисперсионный анализ влияния срока испытаний

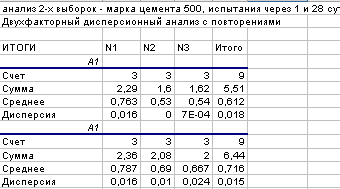
Для цемента марки 400 существенное влияние на коэффициент однородности бетона оказывает срок испытания и практически не влияет «период изготовления». Взаимодействие этих факторов статистически незначимо.

Для марки цемента 500 наблюдается обратная картина: срок испытания не оказывает существенного влияния на коэффициент однородности и заметное влияние оказывает «период изготовления». Взаимодействие этих факторов статистически незначимо.

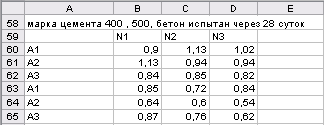
Для анализа влияния на коэффициент однородности бетона марки цемента из таблицы 2.22 сформированы таблицы 2.26 и 2.27.

Т а б л и ц а 2.26

Информация для анализа влияния основных факторов

и марки цемента

Т а б л и ц а 2.27

Информация для анализа влияния основных факторов

и марки цемента

Т а б л и ц а 2.28

Дисперсионный анализ влияния марки цемента

Т а б л и ц а 2.29

Дисперсионный анализ влияния марки цемента

При испытании образцов бетона через 28 суток существенное влияние на коэффициент однородности оказывает марка цемента, не влияют «периоды изготовления» бетона и их взаимодействие. При испытании образцов бетона через сутки существенное влияние на коэффициент однородности оказывают марка цемента и «периоды изготовления» и не оказывает влияние их взаимодействие.

Сводка дисперсионного анализа всех выборок таблицы 2.22 представлена в таблице 2.30.

Как следует из таблицы 2.30, наиболее значимыми факторами являются марка цемента, срок испытания, «период изготовления» бетона и незначимо их взаимодействие.

Среднее значение коэффициента однородности бетона уменьшается с изменением марки цемента: =0,757 и =0,612 при испытании через сутки; =0,952 и =0,715 при испытании через 28 суток, т.е. с увеличением возраста бетона коэффициент однородности увеличивается, что объясняется стабилизацией структурообразования и снятием термических напряжений.

Т а б л и ц а 2.30

Общий дисперсионный анализ выборок

Следовательно, с помощью инструмента Двухфакторный дисперсионный анализ с повторениямиможно проводить многофакторный дисперсионный анализ.