Расчет передачи с зацеплением Новикова на контактную прочность

Этот расчет производят по аналогичным расчетным формулам на контактную прочность для косых зубьев эвольвентного зацепления, но с учетом их большей нагрузочной способности. На основании опытных данных несущую способность зубьев зацепления Новикова по контактной прочности принимают в 1,75-2 раза больше, чем для эвольвентных зацеплений.

Условия контакта в передачах с зацеплением Новикова отличаются от условий контакта по Герцу (малая разность r₁ и r₂большие значения 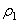и ). Учитывается экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев.

Контактные напряжения приближаются к напряжениям смятия. Рас­чет передач Новикова по контактным напряжениям применяют условно и ведут аналогично расчету с эвольвентным зацеплением.

Для зацепления Новикова коэффициент К_а = 33,6 МПа^1/3, а при расчете эвольвентной передачи К_а = 49,5...43 МПа^1/3. Это объясняется тем, что не­сущая способность зубьев с зацеплением Новикова в 1,75-2 раза больше по сравнению с эвольвентными передачами.

Ширина колеса не влияет на прочность зубьев на излом при зацепле­нии Новикова. В передачах с зацеплением Новикова нагрузка, распреде­ленная на площадке контакта, приложена не по всей длине зуба, как это имеет место в эвольвентном зацеплении, а лишь на сравнительно неболь­шом его участке. При этом значительная часть зуба практически ее не вос­принимает. Следовательно, изменение ширины венца колеса b при неиз­менном угле наклона зуба в отличие от эвольвентных колес практически не сказывается на прочности зубьев на излом.

Планетарные зубчатые передачи. Устройство передачи и расчет на прочность

Передачи, имеющие зубчатые или фрикционные колеса с перемещающимися осям, называют планетарными. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Наиболее распространена зубчатая однорядная планетарная передача (рис.60). Она состоит из центрального колеса 1 с наружными зубьями, неподвижного (центрального) колеса 2 с внутренними зубьями и водила на котором закреплены оси планетарных колес g (или сателлитов).

Рис.60. Планетарная передача

Водило вместе с сателлитами вращается вокруг центральной оси, а са­теллиты обкатываются по центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет. При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.

Планетарную передачу, совершаемую подвижными звеньями (оба иентральных колеса и водило), называют дифференциалом. С помощью диффе­ренциала одно движение можно разложить на два или два движения сло­жить в одно: от колеса 2 движение можно передавать одновременно колесу 1 и водилу h или от колес 1 и 2 к водилу g и т. д. Планетарную передачу ус­пешно применяют в транспортном машиностроении, станкостроении, приборостроении.

Достоинства и недостатки планетарных передач.

Основное достоинство — широкие кинематические возможности, по­зволяющие использовать передачу в качестве редуктора коробки скоро­стей, передаточное число в которой изменяется путем поочередного тормо­жения различных звеньев, и как дифференциальный механизм.

- Планетарный принцип позволяет получать большие передаточные чис­ла (до тысячи и больше) без применения многоступенчатых передач.

- Эти передачи компактные и имеют малую массу. Переход от простых передач к планетарным позволяет во многих случаях снизить их массу в 4 раза и более.

- Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.

- Эти передачи работают с меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и регулирование скорости;

- Имеют малый шум вследствие замыкания сил в механизме.

Основные недостатки: повышенные требования к точности изготовле­ния и монтажа (для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом); резкое снижение КПД передачи с увеличением передаточ­ного отношения.

Передаточное отношение.

Для определения передаточного отношения планетарной передачи ис­пользуется метод Виллиса — метод останова водила.

Передаточное отношение планетарной передачи (см. рис. 60)

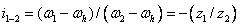(33)

где и 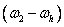— угловые скорости колес 1 и 2 относительно води­ла h; и — числа зубьев этих колес.

Для реальной планетарной передачи (колесо 2 закреплено неподвиж­но, колесо 1 — ведущее, водило h ведомое) при 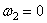из формулы (36) получим

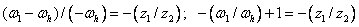
или

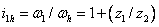(34)

Для однорядной планетарной передачи , для многоступен­чатых 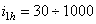, для кинематических передач 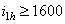.Чем больше передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).

Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с расчетом обыкновенных зубчатых передач от­дельно для каждого зацепления (см. рис.60): пара колес 1—g (внешнее зацепление) и g—2 — (внутреннее). Для таких передач достаточно рассчи­тать только внешнее зацепление, так как модули и силы в зацеплениях одинаковые, а внутреннее зацепление прочнее внешнего.

Проектировочный расчет планетарной передачи на контактную ус­талость активных поверхностей зубьев проводится по следующей формуле:

(35)

где d₁ — делительный диаметр ведущего звена (шестерни), мм; K_d = 78 МПа — вспомогательный коэффициент (рассматриваются сталь­ные прямозубые колеса); T₂ — вращающий момент на шестерне, Нмм; 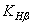— коэффициент нагрузки (см. табл.4); 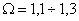— коэффици­ент, учитывающий неравномерность распределения нагрузки среди сател­литов; 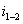— передаточное отношение; 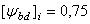— коэффициент длины зуба (ширины колеса); 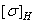— допускаемое контактное напряжение, МПа.

При расчете планетарных передач выбор числа зубьев колес зависит не только от передаточного отношения , но и от условий собираемости пере­дач. При этом сумма зубьев центральных колес должна быть кратной числу сателлитов (лучше 3).