Пример выполнения задания. На участке трубы AB на груз D действует постоянная сила , направление которой показано на рис

2.3.1. Условие примера

На участке трубы AB на груз D действует постоянная сила , направление которой показано на рис. 2.2, и сила сопротивления . Длина участка AB=l. На участке BC на груз действует сила трения F_TP (коэффициент трения f=0,1) и переменная сила , где F измеряется в ньютонах, а t - в секундах.

Определить уравнение движения груза D на участке BC при следующих значениях параметров: m=4кг, Q=10H, m=0,8Hc²/м², n=2, V₀=12м/c, l=2,5м, g=9,9м/c².

2.3.2. Решение примера

Дифференциальное уравнение движения груза D на участке АВ
( рис.2.3) запишется

Начальные условия ( ): м/с.

При прямолинейном движении скорость точки , а ускорение .

Тогда дифференциальное уравнение движения груза D примет вид:

.

Отсюда получаем:

Производную представим в виде:

.

Тогда получим следующее дифференциальное уравнение с разделяющимися переменными:

.

Разделив переменные, имеем

.

Интегрирование этого дифференциального уравнения дает:

.

После подстановки пределов интегрирования, получаем:

.

Потенцируя обе части последнего равенства, находим скорость груза D в конце участка AB:

м/с.

Запишем дифференциальное уравнение движения груза D на участке BС (рис.2.3):

,

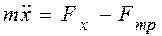где .

;

.

Начальные условия:

, м/с.

При прямолинейном движении и , поэтому имеем:

.

Разделяем переменные

.

После интегрирования, получим:

.

Из второго начального условия:

;

м/с.

Следовательно,

.

Но , поэтому .

Отсюда, после разделения переменных, имеем:

.

И, после интегрирования, получим:

.

Из первого начального условия:

м.

Окончательно имеем:

(м).