
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения задания. Тело D, имеющее форму прямоугольной пластины, показанной на рис
4.3.1. Условие примера
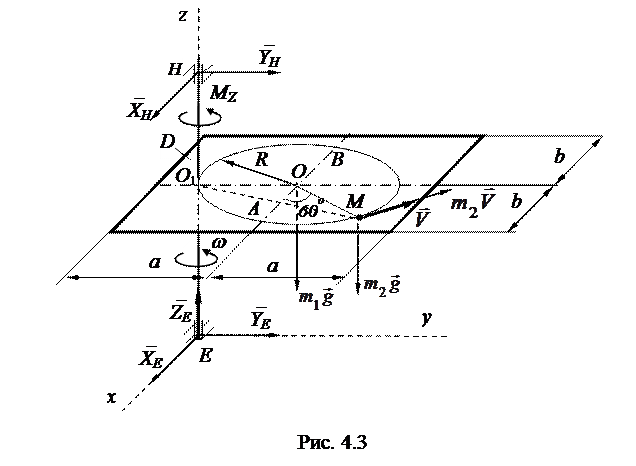
Тело D, имеющее форму прямоугольной пластины, показанной на рис. 4.2, массой 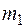 =20 кг вращается вокруг вертикальной оси z с угловой скоростью
=20 кг вращается вокруг вертикальной оси z с угловой скоростью  =2 с-1. При этом в точке M желоба AB тела D на расстоянии ÈAM=
=2 с-1. При этом в точке M желоба AB тела D на расстоянии ÈAM= 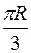 от точки A, отсчитываемом вдоль желоба, закреплена материальная точка K массой
от точки A, отсчитываемом вдоль желоба, закреплена материальная точка K массой  =8 кг. В момент времени
=8 кг. В момент времени 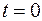 на систему начинает действовать пара сил с моментом
на систему начинает действовать пара сил с моментом 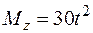 Нм. При t=t1=4 с действие пары сил прекращается; одновременно точка K начинает относительное движение по желобу согласно закону
Нм. При t=t1=4 с действие пары сил прекращается; одновременно точка K начинает относительное движение по желобу согласно закону 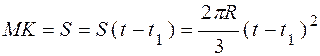 м.
м.
Определить угловые скорости тела D соответственно в моменты времени 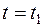 и t=t2=5 с, если R=0,6 м, a=1,2 м; b=0,9 м
и t=t2=5 с, если R=0,6 м, a=1,2 м; b=0,9 м

4.3.2. Решение примера
Запишем равенство, выражающее теорему об изменении кинетического момента механической системы относительно оси z
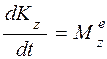 , (4.1)
, (4.1)
где 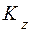 - кинетический момент механической системы, состоящей в данном случае из кинетического момента тела D и кинетического момента точки К, относительно оси z;
- кинетический момент механической системы, состоящей в данном случае из кинетического момента тела D и кинетического момента точки К, относительно оси z;
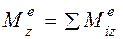 - главный момент внешних сил, приложенных к системе, относительно оси z.
- главный момент внешних сил, приложенных к системе, относительно оси z.
Рассмотрим движение системы в отрезке времени [0;t1].
В произвольный момент времени на систему действуют внешние силы 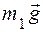 ,
,  ,
, 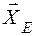 ,
, 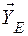 ,
,  ,
, 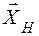 ,
, 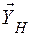 ,
, 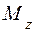 (рис. 4.3), главный момент которых относительно оси z равен вращающему моменту
(рис. 4.3), главный момент которых относительно оси z равен вращающему моменту 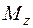 , то есть
, то есть
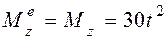 . (4.2)
. (4.2)
Кинетический момент данной системы равен сумме
 ,
,
где 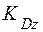
 - кинетические моменты тела D и точки K относительно оси z.
- кинетические моменты тела D и точки K относительно оси z.
Тело D вращается относительно неподвижной оси, поэтому
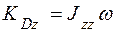 .
.
Здесь 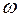 - угловая скорость тела, а
- угловая скорость тела, а 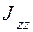 - его момент инерции относительно оси z.
- его момент инерции относительно оси z.
Момент инерции  тела относительно оси
тела относительно оси  , параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл. 4.2)
, параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл. 4.2)
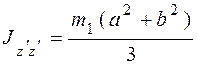 .
.
По теореме Штейнера
 .
.
Таким образом
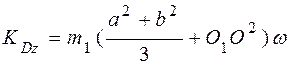 .
.
Кинетический момент материальной точки K, закрепленной в точке М желоба
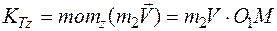 .
.
Скорость точки К
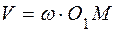 .
.
Очевидно, что 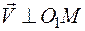 .
.
Согласно условию задачи длина дуги окружности 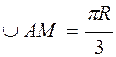 , тогда центральный угол
, тогда центральный угол 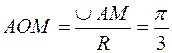 . Следовательно, в равнобедренном треугольнике ОМО1
. Следовательно, в равнобедренном треугольнике ОМО1 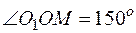 и
и  .
.
Имеем
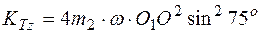 .
.
Окончательное выражение кинетического момента системы относительно оси z следующее
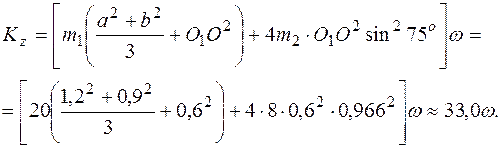 (4.3)
(4.3)
Подставляя выражения (4.2) и (4.3) в равенство (4.1), имеем
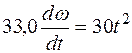 ,
,
откуда
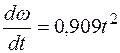 .
.
Разделяем в последнем уравнении переменные и интегрируем левую и правую части уравнения:
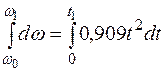 .
.
Тогда
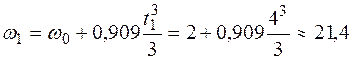 с-1.
с-1.
В момент времени t1 из выражения (4.3) имеем
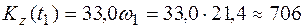 Нмс.
Нмс.
Рассмотрим теперь движение системы в отрезке времени 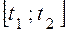 .
.
После прекращения действия момента 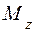 на тело D, главный момент внешних сил относительно оси z
на тело D, главный момент внешних сил относительно оси z  (см. рис. 4.4).
(см. рис. 4.4).
Тогда равенство (4.1) примет вид
 ,
,
то есть 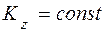 .
.
Это означает, что кинетические моменты системы относительно оси в начале t1 и в конце t2 отрезка времени [t1; t2] равны
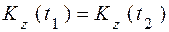 .
.

В момент времени t2 тело D вращается с угловой скоростью  (см. рис. 4.4). При этом точка К, совершая сложное движение, оказывается в точке В желоба. Действительно, центральный угол
(см. рис. 4.4). При этом точка К, совершая сложное движение, оказывается в точке В желоба. Действительно, центральный угол
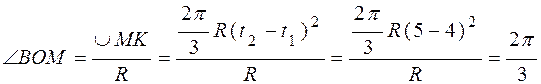 .
.
Кинетический момент системы 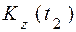 относительно оси в конце t2 отрезка времени [t1; t2] также равен сумме кинетических моментов тела
относительно оси в конце t2 отрезка времени [t1; t2] также равен сумме кинетических моментов тела  и точки
и точки 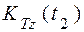 :
:
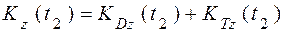 .
.
Очевидно, что
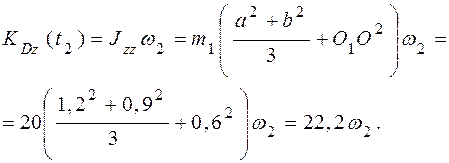
По теореме о сложении скоростей:
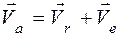 ,
,
где 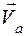 ,
, 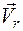 ,
, 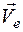 - абсолютная, относительная и переносная скорости точки.
- абсолютная, относительная и переносная скорости точки.
Умножая обе части этого равенства на m2, получаем:
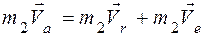 .
.
Следовательно, кинетический момент точки К в конце отрезка времени t2 равен сумме моментов векторов  и
и 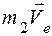 относительно оси z
относительно оси z

Относительная скорость точки К
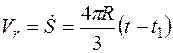 .
.
При t=t2=5 c найдем величину относительной скорости точки К
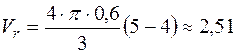 м/с.
м/с.
Переносная скорость точки К
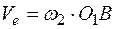 .
.
Из прямоугольного треугольника О1ОВ по теореме Пифагора имеем:
 .
.
Окончательно получаем
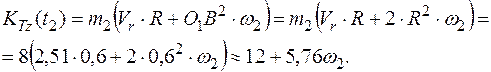
Тогда
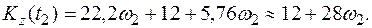
Приравнивая  и
и  :
:
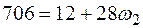 ,
,
находим
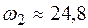 с-1.
с-1.
Дата добавления: 2015-02-09; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |