
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения задания. Груз А прикрепленный к горизонтальной пружине совершает горизонтальные колебания под действием возмущающей силы
3.3.1. Условие примера
Груз А прикрепленный к горизонтальной пружине совершает горизонтальные колебания под действием возмущающей силы  , как показано на рис. 3.1.
, как показано на рис. 3.1.
Масса груза m=0,8 кг, амплитуда возмущающей силы
 =28,8 Н, ее круговая частота
=28,8 Н, ее круговая частота  с-1, начальные условия движения груза на пружине
с-1, начальные условия движения груза на пружине  м,
м,  м/с.
м/с.
Определить коэффициент с упругости пружины для значения коэффициента динамичности  при
при  .
.
Найти уравнение движения груза при заданных начальных условиях и найденном значении коэффициента упругости пружины. Начало отсчета на оси взять на конце недеформированной пружины.
Построить график зависимости амплитуды вынужденных колебаний от коэффициента расстройки для значений 0; 0,25; 0,5; 0,75; 0,9; 1,0; 1,1; 1,25; 1,5; 1,75; 2,0.
При решении задачи считать, что сила упругости пружины прямо пропорциональна ее деформации, а силами сопротивления движению пренебречь.
Определить зависимость амплитуды вынужденных колебаний от сопротивления движению, считая силу сопротивления пропорциональной величине скорости груза. При значении коэффициента затухания  с-1, построить график зависимости амплитуды вынужденных колебаний от коэффициента расстройки
с-1, построить график зависимости амплитуды вынужденных колебаний от коэффициента расстройки  для значений 0; 0,25; 0,5; 0,75; 0,9; 1,0; 1,1; 1,25; 1,5; 1,75; 2,0.
для значений 0; 0,25; 0,5; 0,75; 0,9; 1,0; 1,1; 1,25; 1,5; 1,75; 2,0.
3.3.2. Решение примера
Определим коэффициент с упругости пружины.
При отсутствии сил сопротивления коэффициент динамичности вычисляется по формуле
 ,
,
откуда
 с-2.
с-2.
С другой стороны, квадрат круговой частоты свободных колебаний без учета сил сопротивления равен
 ,
,
следовательно
 Н/м.
Н/м.
Амплитуда вынужденных колебаний определяется произведением
 .
.
Здесь  - деформация пружины при статическом действии силы
- деформация пружины при статическом действии силы  .
.
В нашем примере
 м,
м,  м.
м.
Силы, приложенные к грузу А в произвольный момент времени, изображены на рис. 3.2

Составляем дифференциальное уравнение движения груза
 (3.1)
(3.1)
где  - сила упругости пружины:
- сила упругости пружины:
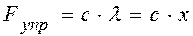 .
.
Подставляя выражения возмущающей силы и силы упругости в уравнение (3.1), получаем следующее дифференциальное уравнение вынужденных колебаний груза:

которое приводится к канонической форме
 (3.2)
(3.2)
Здесь  м/с2.
м/с2.
Это дифференциальное уравнение необходимо решать при начальных условиях:
 м, (3.3)
м, (3.3)
 м/с.
м/с.
Общее решение уравнения (3.2) является суммой двух функций
 ,
,
где  - общее решение однородного уравнения, а
- общее решение однородного уравнения, а  - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Однородное уравнение имеет решение
 ,
,
где и  и
и  - постоянные интегрирования.
- постоянные интегрирования.
Частное решение неоднородного уравнения следующее
 .
.
Таким образом, в нашем примере
 . (3.4)
. (3.4)
Постоянные интегрирования находим из начальных условий (3.3).
Подставляя функцию (3.4) в первое начальное условие, имеем:
 ,
,
откуда
 м.
м.
Далее определяем производную по времени от функции (3.4)
 .
.
Тогда из второго начального условия (3.3), следует
 .
.
Получаем
 м.
м.
Уравнение колебательного движения груза А окончательно примет вид
 , м.
, м.
Зависимость амплитуды вынужденных колебаний от коэффициента расстройки следующая
 (3.5)
(3.5)
Результаты вычислений по формуле (3.5) для различных значений z приведены в табл. 3.2.
Таблица 3.2
| z | 0,25 | 0,5 | 0,75 | 0,9 | 1,0 | 1,1 | 1,25 | 1,5 | 1,75 | 2,0 | |
| В×102, м | 1,0 | 1,07 | 1,33 | 2,29 | 5,26 | ¥ | 4,76 | 1,78 | 0,8 | 0,485 | 0,333 |
По данным табл. 3.2 строим кривую 1 на рис. 3.3, которая называется амплитудно–частотной характеристикой системы при отсутствии сопротивления.
При наличии силы сопротивления окружающей среды, пропорциональной скорости груза, дифференциальное уравнение движения системы будет иметь вид
 ,
,
где n – коэффициент затухания (с-1).
Величина амплитуды вынужденных колебаний находится по формуле
 (3.6)
(3.6)
где  - относительный коэффициент затухания
- относительный коэффициент затухания  .
.
В нашем случае  .
.
Результаты вычислений по формуле (3.6) для различных значений z приведены в табл. 3.
Таблица 3.3
| z | 0,25 | 0,5 | 0,75 | 0,9 | 1,0 | 1,1 | 1,25 | 1,5 | 1,75 | 2,0 | |
| В×102, м | 1,0 | 1,06 | 1,29 | 1,89 | 2,46 | 2,5 | 2,05 | 1,33 | 0,72 | 0,459 | 0,322 |
По данным табл. 3.3 строим кривую 2 на рис. 3.3, которая дает представление о влиянии сопротивления на амплитуду вынужденных колебаний груза.
 |




Дата добавления: 2015-02-09; просмотров: 381; Мы поможем в написании вашей работы!; Нарушение авторских прав |