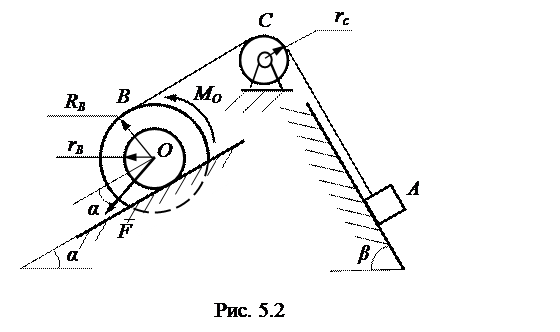
Пример выполнения задания. Рассматривается движение механической системы, изображенной на рис

5.3.1. Условие примера

Рассматривается движение механической системы, изображенной на рис. 5.2. Даны следующие значения параметров: 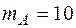кг, кг, кг, Н, Нм,
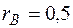м, м, 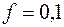м, м, , , , м, м, м/с².

Определить скорость 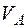и ускорение тела А.

5.3.2. Решение примера

Равенство, выражающее теорему об изменении кинетической энергии механической системы, имеет вид

, (5.1)

где и - кинетическая энергия системы в начальном и конечном положениях,

и 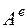- суммарные работы внутренних и внешних сил, приложенных к системе, при ее переходе из первого положения во второе.

На рис. 5.3 условно изображены начальное и конечное положения данной системы.

Согласно условию задачи система начинает движение из состояния покоя, поэтому .

Кроме того, поскольку тела, образующие систему, абсолютно твердые и трос не растягивается, то .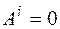

Таким образом, равенство (5.1) запишется

. (5.2)

Кинетическая энергия системы равна

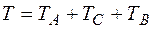
Груз А движется поступательно со скоростью 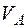, поэтому

(5.3)

Шкив С вращается с угловой скоростью , следовательно,

(5.4)

Момент инерции шкива С относительно оси, проходящей через точку О₁, определяется по формуле:

(5.5)

Угловая скорость шкива С равна

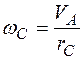. (5.6)

Подставляя выражения (5.5) и (5.6) в равенство (5.4), получаем:

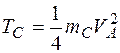. (5.7)

Кинетическую энергию колеса В, совершающего плоское движение, находим по формуле:

. (5.8)

Здесь - линейная скорость центра О масс колеса В,

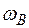- мгновенная угловая скорость колеса В,

- момент инерции колеса В относительно оси, проходящей через центр О.

На рисунке 5.3 буквой обозначен мгновенный центр скоростей колеса В. Очевидно, что мгновенная угловая скорость колеса В

.

Но для нормальной работы системы скорости 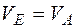, а , тогда

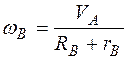. (5.9)

Скорость центра О колеса В равна

. (5.10)

Момент инерции колеса В равен

. (5.11)

После подстановки выражений (5.9) и (5.10) в формулу (5.8), получаем:

. (5.12)

Далее, суммируя выражения (5.3),(5.7) и (5.12), окончательно имеем

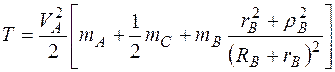. (5.13)

Внешние силы, действующие на рассматриваемую механическую систему, показаны на рисунке 5.3. Причем сила трения скольжения действующая на тело А имеет максимальное значение, которое находится по формуле Кулона:

. (5.14)

Здесь 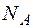- нормальная реакция плоскости находится по формуле

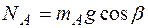. (5.15)

Суммарная работа внешних сил действующих на рассматриваемую механическую систему равна

(5.16)

Работа силы тяжести 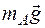тела А:

. (5.17)

Работа максимальной силы трения скольжения 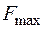тела А:

.

С учетом равенств (5.14) и (5.15), последнее выражение примет вид

. (5.18)

Работа нормальной реакции :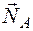

, (5.19)

так как .

Точки приложения сил 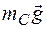и не перемещаются, поэтому

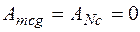. (5.20)

Работа силы тяжести 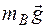колеса В:

. (5.21)

Работа постоянной силы :

. (5.22)

Работа постоянного момента :

. (5.23)

Работа нормальной реакции 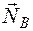наклонной плоскости:

, (5.24)

так как эта сила перпендикулярна вектору перемещения ее точки приложения.

Сила трения скольжения колеса В приложена в мгновенном центре скоростей колеса В, поэтому:

. (5.25)

Работа максимально момента трения качении :

. (5.26)

Величина максимального момента трения качения дается формулой

. (5.27)

Для определения зависимостей перемещения 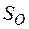центра О и угла 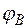поворота колеса В от перемещения тела А умножим обе части выражений (5.9), (5.10) на . Имеем

, .

Или

, .

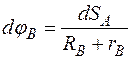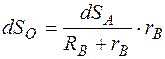Интегрируя обе части последних двух уравнений, получаем

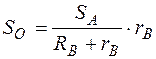, . (5.28)

Подставляя выражения (5.17)-(5.26) в сумму (5.16), с учетом формул (5.27), (5.28), имеем

(5.29)

Тогда равенство (5.2) с учетом выражений (5.13) и (5.29) примет вид

.

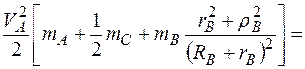
Отсюда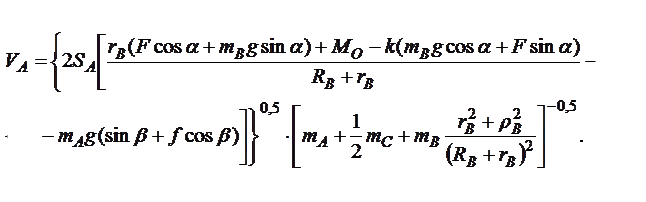

Для определения ускорения тела А продифференцируем обе части равенства (5.30) по времени t. Имеем

Поскольку

и ,

то

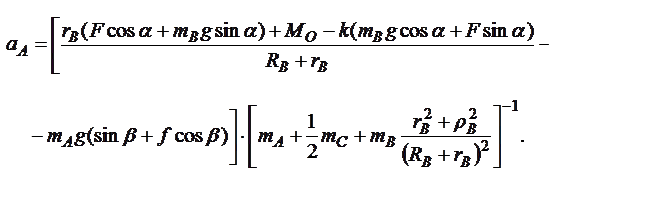
Таким образом, для заданных числовых значений параметров, скорость и ускорение тела А равны:

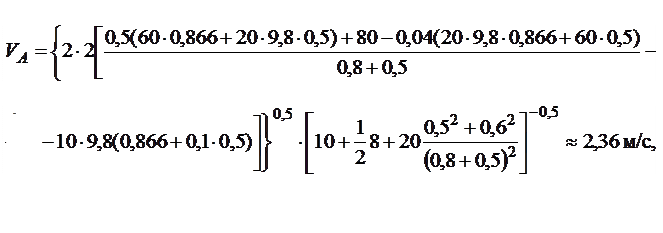
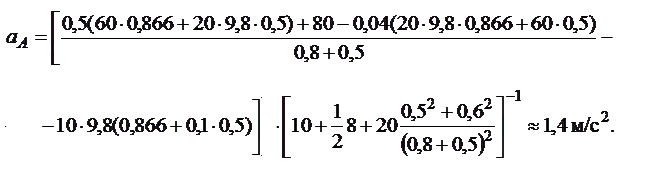Дата добавления: 2015-02-09; просмотров: 6; Нарушение авторских прав