
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание №6. Применение уравнений Лагранжа второго рода к изучению движения механической системы с двумя степенями свободы
Содержание задания
Тело  массой
массой  вращается вокруг вертикальной оси
вращается вокруг вертикальной оси  под действием пары сил с моментом
под действием пары сил с моментом  . Варианты расчетных схем изображены на рис. 7.1. При этом по желобу
. Варианты расчетных схем изображены на рис. 7.1. При этом по желобу  тела
тела  под действием внутренней силы
под действием внутренней силы  , направленной по касательной к желобу (управляющее воздействие), движется материальная точка
, направленной по касательной к желобу (управляющее воздействие), движется материальная точка 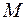 массой
массой 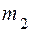 . Согласно закону равенства действия и противодействия с такой же по величине силой, но направленной в противоположную сторону, точка
. Согласно закону равенства действия и противодействия с такой же по величине силой, но направленной в противоположную сторону, точка 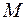 действует на тело
действует на тело  . Варианты числовых значений параметров приведены в табл. 7.1.
. Варианты числовых значений параметров приведены в табл. 7.1.
Используя уравнения Лагранжа второго рода, составить дифференциальные уравнения движения механической системы в обобщенных координатах. Сопротивлением движению пренебречь.
Тело D рассматривать как тонкую однородную пластину. Форма пластины выбирается в соответствии с вариантом задачи
(см. рис. 7.1). Осевой момент инерции тела определять по формуле приведенной в табл. 4.2.
Дата добавления: 2015-02-09; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |