
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения задания. Изучается движение механической системы, представленной на рис
7.3.1. Условие примера
Изучается движение механической системы, представленной на рис. 7.2. Даны следующие значения параметров: 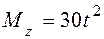 Нм,
Нм,  Н,
Н,  кг,
кг,  кг,
кг, 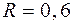 м,
м,  м,
м, 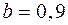 м.
м.

73.2. Решение примера
Рассматриваемая механическая система имеет две степени свободы (n=2). В качестве обобщенных координат назначим угол  поворота пластины вокруг вертикальной оси
поворота пластины вокруг вертикальной оси  и центральный угол
и центральный угол  , определяющий положение материальной точки
, определяющий положение материальной точки 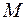 на круговом желобе
на круговом желобе  (рис. 7.3).
(рис. 7.3).

Уравнения Лагранжа второго рода для данной механической системы могут быть представлены в виде:
 ,
,
(7.1)
 .
.
Здесь  - кинетическая энергия системы,
- кинетическая энергия системы, 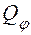 и
и  - обобщенные силы, соответствующие назначенным обобщенным координатам.
- обобщенные силы, соответствующие назначенным обобщенным координатам.
Кинетическая энергия системы равна сумме кинетической энергии пластины  и материальной точки
и материальной точки  :
:

Пластина совершает вращательное движение вокруг неподвижной оси  , поэтому:
, поэтому:
 .
.
Момент инерции пластины относительно оси  определяем по теореме Штейнера.
определяем по теореме Штейнера.
Имеем
 .
.
Таким образом,
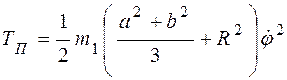 .
.
Кинетическая энергия материальной точки равна
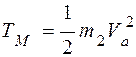 ,
,
где  - абсолютная скорость точки
- абсолютная скорость точки 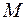 .
.
По теореме о сложении скоростей
 .
.
Величина относительной скорости 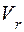 точки
точки 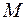
 . (7.2)
. (7.2)
Переносная скорость  точки
точки 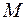
 . (7.3)
. (7.3)
Векторы 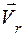 и
и 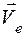 изображены на рис.7.3. Очевидно, что:
изображены на рис.7.3. Очевидно, что:
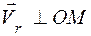 ,
,  и
и  .
.
Квадрат модуля абсолютной скорости точки 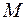 вычисляется по формуле
вычисляется по формуле

Тогда с учетом равенств (7.2) и (7.3), получаем
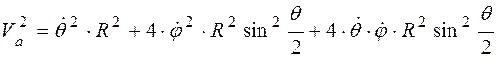 .
.
Кинетическая энергия точки 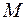
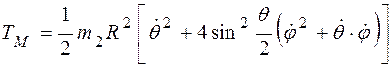 .
.
Окончательное выражение кинетической энергии системы
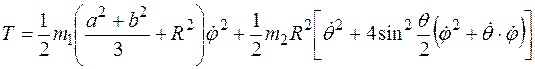 (7.4)
(7.4)
Для определения обобщенных сил 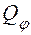 и
и  сообщаем системе возможные перемещения.
сообщаем системе возможные перемещения.
Первое возможное перемещение:


Сумма работ активных сил на этом возможном перемещении равна
 .
.
Тогда
 . (7.5)
. (7.5)
Второе возможное перемещение:

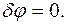
В этом случае сумма работ активных сил запишется
 .
.
Следовательно,
 . (7.6)
. (7.6)
Вычисляем частные производные от функции (7.4) кинетической энергии по обобщенным скоростям:
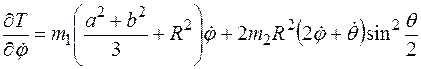 , (7.7)
, (7.7)
 (7.8)
(7.8)
Далее находим обыкновенные производные по времени от полученных выражений (7.7) и (7.8):
 (7.9)
(7.9)
 (7.10)
(7.10)
Затем вычисляем частные производные от кинетической энергии (7.4) по обобщенным координатам:
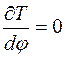 ,
,  (7.11)
(7.11)
Подставляя равенства (7.5),(7.6),(7.9)--(7.11) в уравнения (7.1), получаем:


С учетом числовых значений исходных данных дифференциальные уравнения движения рассматриваемой механической системы примут вид:
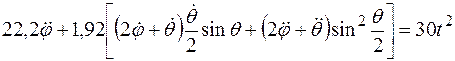 ,
,
 .
.
Дата добавления: 2015-02-09; просмотров: 242; Мы поможем в написании вашей работы!; Нарушение авторских прав |