Вычисление определенных интегралов

Задание.

Найти значение определенного интеграла методами, указанными преподавателем.

Пример.

Найти значение определенного интеграла тремя методами (по формулам прямоугольников , трапеций и Симпсона). Оценить погрешность по правилу Рунге.

Выполнение работы.

Формула левых прямоугольников :

, ( 1 )

где , , 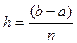n-число интервалов разбиения .

Формула трапеций :

( 2 )

Формула Симпсона :

, ( 3 )

где 2n-четное число интервалов разбиения.

1. Введем число интервалов разбиения в ячейку В2 (для формулы Симпсона оно должно быть четным, поэтому выберем 10) , нижний предел интегрирования - в С2 , верхний предел - в D2. Шаг вычислим по формуле =(D2-C2)/B2 в ячейке Е2. В ячейку А4введем ссылку на С2 , а в А5 введем формулу вычисления аргумента =А4+$E$2. Распространим ее вниз на необходимое количество ячеек. Для этого захватим курсором мыши маркер в правом нижнем углу рамки выделения ячейки A5 и перетащим его вниз на необходимое число ячеек. Полученный столбец значений аргумента озаглавим “Х” в ячейке А3. В ячейку В4 введем формулу, вычисляющую подынтегральную функцию =cos(A4), и распространим ее аналогичным способом вниз. Полученный столбец озаглавим “Y” в ячейке В3.

2. В ячейку С4 вставим формулу =В4.Эта ссылка избавит нас от лишних вычислений. Распространим формулу до ячейки С14 включительно. В ячейке С15 найдем значение интеграла методом прямоугольников, введя формулу =СУММ(C4:C14)*$E$2.

3. Для того , чтобы найти значение интеграла по формуле трапеций, вставим в ячейку D4 ссылку на В4. Распространим ее вниз на необходимое число строк. Отредактируем формулы в ячейках D4 и D13 в соответствии с формулой трапеций ( 2 ). В ячейке С14 найдем значение интеграла по формуле трапеций , вычислив сумму и умножим ее на шаг.

4. Для нахождения интеграла по формуле Симпсона сформируем столбец Е4:Е13 аналогично предыдущему пункту. Отредактируем формулы в соответствии с формулой Симпсона (3 ). В ячейке D14 найдем значение интеграла по формуле =СУММ(E4:E14)*$E$2/3.

5. Для оценки погрешности вычислений по правилу Рунге необходимо вычислить значение интеграла с удвоенным шагом. Применим эту процедуру к вычислениям по формуле Симпсона. В область F4:F14скопируем через одну формулы из области E4:E14 и отредактируем их в соответствии формулой (3 ). В ячейке F15 получим значение интеграла по формуле Симпсона с удвоенным шагом. В ячейку F16 вводим формулу =ABS(F15-E15)/15для оценки погрешности.

6. Полученная таблица представлена на рисунке 15.

Рис. 15. Результаты численного интегрирования.