КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обработка экспериментальных данных
Задание.
1. Провести сглаживание экспериментальных данных.
2. Аппроксимировать экспериментальные данные по методу наименьших квадратов.
Пример 5.1.
Провести сглаживание экспериментальных данных, заданных таблицей:
Отобразить полученные результаты на диаграмме.
Выполнение работы.
Сглаживание данных эксперимента является специальной операцией усреднения с помощью интерполяционных полиномов, которая обеспечивает получение усредненного значения yi* по заданному значению yi и ряду близлежаших значений (..., yi-2, yi-1, yi+1, yi+2, ...), известных с некоторой погрешностью. При этом используются следующие вычислительные схемы (n - число экспериментальных точек, yi* - сглаженные значения) :
· линейное сглаживание по трем точкам:
y0*=(5*y0+2*y1-y2)/6
yi*=(yi-1+yi+yi+1)/3 , 1 £ i £ n-1
yn*=(5*yn+2*yn-1-yn-2)/6
· Линейное сглаживание по пяти точкам:
y0*=(3*y0+2*y1+y2-y4)/5
y1*=(4*y0+3*y1+2*y2+y3)/10
yi*=(yi-2+yi-1+yi+ yi+1+yi+2)/5, где2 £ i £ n-2
yn-1*=(yn-3+2*yn-2+3*yn-1+4*yn)/10
yn*=(3*yn+2*yn-1+yn-2-yn-4)/5
· Нелинейное сглаживание по семи точкам:
y0*=(39y0+8y1-4(y2+y3-y4)+y5-2y6)/42
y1*=(8y0+19y1+16y2+6y3-4y4-7y5+4y7)/42
y2*=(-4y0+16y1+19y2+12y3+2y4-4y5+y6)/42
yi*=(7yi+6(yi+1+yi-1)+3(yi+2+yi-2)-2(yi+3+yi-3))/21 , 3 £ i £ n-3
yn-2*=(yn-6-4yn-5+2yn-4+12yn-3+19yn-2+16yn-1-4yn)/42
yn-1*=(4yn-6-7yn-5-4yn-4+6yn-3+16yn-2+19yn-1+8yn)/42
yn*=(-2yn-6+4yn-5+yn-4-4yn-3-4yn-2+8yn-1+39yn)/42
Будем использовать линейное сглаживание по трем точкам.
Введем значения аргументов, допустим, в столбец А, а экспериментальные значения в столбец В, начиная со второй строки (первую строку отведем под заголовки столбцов).
В ячейку С2 введем формулу =(5*B2+2*B3-B4)/6. Это будет точка y0.
В ячейку С3 записываем формулу =(B2+B3+B4)/3для yi. Захватываем курсором мыши маркер распространения и распространяем эту формулу на 6 строк вниз (8 - количество экспериментальных данных).
В ячейку С9 вводим последнюю формулу =(5*B9+2*B8-B7)/6.
Результаты представим в виде диаграммы.
Полученная электронная таблица показана на рисунке 18.
Рис. 18. Результаты сглаживания экспериментальных данных.
Пример 5.2.
Аппроксимировать кубическим полиномом функцию, заданную следующей таблицей:
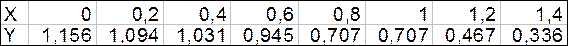
Отобразить полученные результаты на диаграмме.
Выполнение работы.
Отыскание параметров аппроксимирующего кубического полинома y=ax3+bx2+cx+d сводится к решению системы линейных уравнений вида
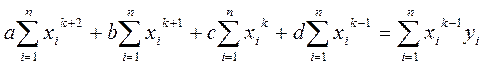, ( 7 )
где k = 1,2,3,4 - номера уравнений, n - число значений в исходной таблице.
Исходные значения x и y занесем в столбцы А и В, начиная со второй строки ( в первой строке поместим заголовки столбцов). Затем для этих столбцов вычислим суммы и поместим их в десятой строке. В столбцах С - J разместим соответственно вычисление и суммирование x i 2, x i 3, x i 4, x i 5, x i 6, x i y i , x i 2 y i , x i 3 y i .
Под полученной таблицей сформируем матрицу коэффициентов и вектор-столбец свободных членов системы ( 7 ).
Решим систему линейных уравнений, как описано в работе 4.
В блоке ячеек J12:J20 вставим формулу =((a*$A2+b)*$A2+c)*$A2+d, вычисляющую на основе полученных коэффициентов значения аппроксимирующего полинома. В следующем столбце вычислим невязку.
Полученная таблица и построенный с помощью Мастера диаграмм график приведены на рисунках 19 и 20.
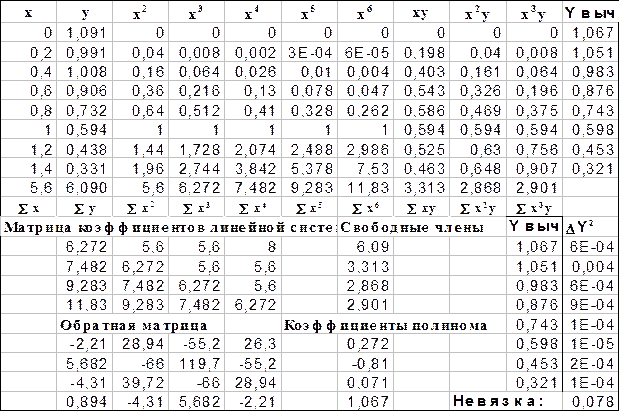
Рис. 19. Таблица вычисления коэффициентов кубического полинома, аппроксимирующего экспериментальные данные.
Рис. 20. Графическое представление результатов аппроксимации экспериментальных данных кубическим полиномом.
Дата добавления: 2015-02-09; просмотров: 224; Мы поможем в написании вашей работы!; Нарушение авторских прав |