Решение систем линейных уравнений. Решить систему линейных уравнений

Задание.

Решить систему линейных уравнений. Выполнить проверку.

Пример.

Требуется решить систему линейных уравнений

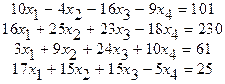( 4 )

Выполнение работы.

Введем обозначения

, , .

Тогда система ( 4 ) запишется в виде

AX = B. ( 5 )

Если матрица А является невырожденной (det A ¹ 0), то система ( 5 ) имеет единственное решение

X= A^-1B. ( 6 )

1. Введем значения коэффициентов при неизвестных, т.е. матрицу А, в блок ячеек A2:D5. Значения свободных членов (матрицу - столбец B) введем в блок F2:F5.

2. В ячейке H2 найдем значение det A. Для этого выделим эту ячейку и вызовем Мастер функций. В окне диалога “Мастер функций - шаг 1 из 2” выберем категорию Мат. и тригонометрия, а в ней функцию МОПРЕД. Нажмем кнопку “Шаг>“ и затем в окне диалога “Мастер функций - шаг 2 из 2” укажем массив A2:D5. Завершим работу с Мастером функций, нажав кнопку “Закончить”. В ячейке H2 получим значение определителя матрицы A, равное 15461.

3. Выделим интервал ячеек A8:D11 для матрицы A^-1. Вызовем Мастер функций, выберем категорию Мат. и тригонометрия, затем функцию МОБР (см. рис. 16).

Рис. 16. Диалоговое окно “Мастер функций - шаг 1 из 2”.

В окне диалога “Мастер функций - шаг 2 из 2” укажем массив A2:D5. После нажатия кнопки “Закончить” получим только один элемент обратной матрицы в левом верхнем углу. Для того, чтобы получить всю обратную матрицу, необходимо для этой ячейки войти в режим редактирования формул и нажать комбинацию клавиш Ctrl+Shift+Enter. Формула в строке редактирования будет заключена в фигурные скобки и распространена на все ячейки выделенной области. В результате мы получим полностью сформированную обратную матрицу.

4. Выделим блок ячеек F8:F11 под вектор-столбец решения, вызовем Мастер функций и с помощью функции МУМНОЖ из категории Мат. и тригонометрия умножим обратную матрицу (A8:D11) на вектор-столбец свободных членов (F2:F5). Для получения всего вектора, как и в предыдущем случае, после нажатия кнопки “Закончить” следует войти в режим редактирования формул и нажать комбинацию клавиш Ctrl+Shift+Enter.

5. Выполним проверку, перемножив матрицы А и B.

Полученная таблица представлена на рис. 17.

Рис. 17. Решение системы линейных уравнений.