Ошибка среднего арифметического

На практике обычно вы-полняется некоторый ряд из n измерений

x₁, x₂, x₃,… x_n. (29)

Этот ряд можно рассмат­ривать как случайную выборку из нормальной генеральной совокупности возможных ре-зультатов с математическим ожиданием М(Х)=Х₀ и диспер- сией :D(х)=σ².

В качестве приближенно­го значения Х₀ целесообразно принять среднее арифмети-ческое из результатов изме-рений:

(30)

Основной задачей теории ошибок является оценка точности приближенного равенства (30).

Среднее арифметическое 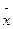случайных величин является также случайной величиной, имеющей нормальное распределение с тем же центром М(Х)=Х₀, но с дисперсией

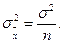(31)

Величину называют средней квадратичной ошибкой среднего арифметического. Следовательно, средняя квадратичная ошибка среднего арифметического из n измерений в раз меньше средней квадратичной ошибки отдельного измерения.

Следует помнить, что σ зависит от обстоятельств измерений изучаемого объекта, инструмента, обстановки измерений и наблюдателя. Поэтому когда характеризуют точность применяемого способа измерения или же сравнивают качество отдельных результатов (выделение промахов), пользуются величиной σ. Когда же оценивают точность окончательного результата измерений (среднего арифметического), применяют .

Остается выяснить, как можно вычислить из опытных данных (29).

Согласно определению (12) дисперсия можно было бы вычислить следующим образом:

однако нам неизвестно истинное значение х₀.

Если Х₀ заменить его приближенным значением 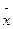, то, как показывает теория, для вычисления дисперсии получится приближенная формула:

(32)

Дисперсию называют выборочной дисперсией, а разность

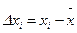(33)

остаточной ошибкой отдельного измерения. Извлекая квадратный корень из (32), получим

(34)

Эта формула, определяющая среднюю квадратичную ошибку по данным случайной выборки, называется формулой Бесселя.

Из выражения (31) аналогично найдем приближенную оценку средней квадратичной ошибки среднего арифметического

(35)

Доверительный интервал и доверительная вероятность (классическая оценка)

Доверительным называют интервал ( ) , который с заданной доверительной вероятностью δ содержит истинное значение Х₀ искомой величина; ( ) и ( ) являются доверительными границами интервала. При этом обычно задаются стандартными значениями доверительной вероятности 0,9; 0,95; 0.99; 0,999.

Доверительной вероятностью называют вероятность δ того, что истинное значение Х₀ измеряемой величины содержится внутри заданного доверительного интервала ( ). При этом δ выражают либо в долях единицы (доверительная вероятность), либо в процентах (надежность).

В классической теории ошибок неизвестные σ и заменяют их приближенными значениями и 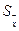; вычисленными из опытных данных по формулам (34) и (35). Доверительную вероятность и доверительный интервал определяют по табл.1 интеграла вероятностей согласно уравнению (27). полагая

(36)

При этом результат измерений принято записывать в краткой символической форме:

(37)

Эту запись следует понимать в том смысле, что истинное значение Х₀ с заданной вероятностью δ находится внутри доверительного интервала ( ).

Классическим методом оценки точности результата измерений можно пользоваться лишь при выборке с большим числом ( 20) измерений.