Параметры распределения случайных величин

Законы распределения являются полными характерис-тиками случайных величин. Но они не всегда удобны для практики. На практике чаще случайную величину характеризуют определенными числовыми параметрами, связанными с законом ее распределения. Основные из них: математическое ожидание и дисперсия. Математическим ожиданием М (X) случайной величины называется сумма произведений всех ее возможных значений на их вероятности:

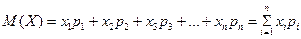(9)

Определение математического ожидания требует знания закона распределения вероятностей. Если он не выявлен, то вычисляют среднее арифметическое значение случайной величины X, т.е.

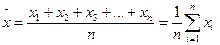(10)

Согласно закону больших чисел :

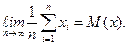(11)

Таким образом, математическое ожидание М(х) является центром распределения вероятностей случайной величины Х и оценивается одним числом, т.е. М(х)= Const.

Отдельные значения случайной величины группируются около математического ожидания как центра (см.рис.I). Степень рассеяния или разброса этих значений характеризуют величиной, называемой дисперсией D(х) случайной величины.

Дисперсией D(х) называют математическое ожидание квадрата отклонений возможных значений случайной величины от ее математического ожидания:

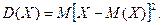(12)

Таким образом, дисперсия предcтавляет средний квадрат отклонений случайной величины от ее математического ожидания. Формулу (12) можно выразить через средние величины в удобной

для вычислений форме:

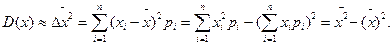(13)

Дисперсия имеет размерность квадрата размерности случайной величины. Поэтому для сопоставления и оценки рассеяния возможных значений случайной величины около математического ожидания вводят понятие среднего квадратичного отклонения, имеющего в отличие от дисперсии такую же размерность, как и случайная величина.

Средним квадратичным отклонением σ случайной величины называют корень квадратный из дисперсии:

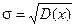(14)

В теории ошибок σ называют средней квадратичной ошибкой.