
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интеграл вероятностей
Интегральная функция нормального распределения результатов измерения F (X) или ошибок F(Δx) в новых переменных будет иметь один и тот же вид:
 (26)
(26)
Вероятность того, что возможный результат измерения Х окажется внутри заданного интервала (Х1, Х2) согласно (26) может быть вычислен по уравнению:

где 

В частности, для симметричного относительно истинного значения Х0 интервала ( 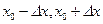 ) получим:
) получим:
 (27)
(27)
Здесь учитывается, что функция  является нечетной.
является нечетной.
Функция 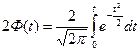 (28)
(28)
называется функцией Лапласа или интегралом вероятностей (табл.1).
Таблица 1
Функция Лапласа 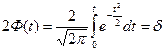
| t | 2Ф(t) | t | 2Ф(t) | t | 2Ф(t) | t | 2Ф(t) |
| 0, | 0,0000 | 1,0 | 0,6827 | 0,9545 | 0,9973 | ||
| 0,5 | 0,3829 | 1,5 | 0,8664 | 2,5 | 0,9876 | 3,5 | 0,9995 |
Интеграл вероятностей (28) по уравнению (27) позволяет вычислять вероятность нахождения результата измерения Х или его ошибки ΔХ в заданном симметричном относительно центра распределения интервала (-σt, σt ). Для этого нужно величину 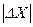 заданного интервале (
заданного интервале ( 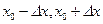 ) или (
) или (  ) выразить в долях σ .т.е. найти
) выразить в долях σ .т.е. найти  и по табл1 определить искомую вероятность
и по табл1 определить искомую вероятность  .
.
Решается и обратная задача. Для заданной вероятности δ (по табл.1) определяют t и по известному σ находят искомый интервал (  ).
).
Найдем значения вероятностей δ для интервалов (  ) при t= I. 2. 3 :
) при t= I. 2. 3 :


 Из последнего равенства следует, что 99,73% всех результатов измерений находятся в пределах интервала
Из последнего равенства следует, что 99,73% всех результатов измерений находятся в пределах интервала
(  ) и лишь 0,27% - за его пределами.
) и лишь 0,27% - за его пределами.
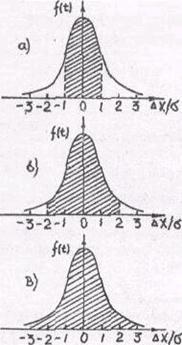
На рис.4 искомые вероятности δ изображены заштрихованными площадями под кривыми Гаусса f(t). Вся площадь код кривой равна единице (на рис. 4а
-t=1, δ=0,68; 4б –t=2, δ=0,95; 4в –t=3, δ=0,997).
Те результаты измерений, ошибки которых вышли за пределы ± 3 σ , имеют очень малую вероятность и такие измерения практически невозможны ("правило трех сигм"). При большом числе отсчетов “правило трех сигм” применяют для выявления грубых ошибок - промахов.
|
Дата добавления: 2014-10-31; просмотров: 375; Мы поможем в написании вашей работы!; Нарушение авторских прав |