Методы учета инструментальных погрешностей

Наиболее распространенными систематическими ошибками являются инструментальные (приборные) погрешности. Количественно они характеризуются предельной допустимой основной погрешностью Δ_пр- практически наибольшей по абсолютной величине воз­можной разностью между показанием (единичным) прибора и истинным значением измеряемой величины. В большинстве случаев Δ_пр определяется классом точности прибора или указывается в инструкции по его применению.

Например, у электроизмерительных приборов класс точности равен отношению погрешности Δ_пр к номинальному (наибольшему) значению шкалы (приведенная погрешность) и обозначается одним из чисел, в %: 0.05; I; 0.2; 0,5; 1.0; 1.5; 2.5; 4. В данном случае, зная класс точности прибора и номинальное значение шкалы, можно определить погрешность Δ_пр, которую мы вынуждены считать постоянной по всей шкале прибора. Так, миллиамперметр класса 0,5 с полной шкалой на 150 мА измеряет пропускаемый ток с ошибкой, не превышающей

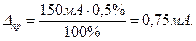
Для приборов, отградуированных по образцовым мерам, базой для определения систематической погрешности яв-ляется оценка ошибки отсчета, которая возможна для данной шкалы измерительного средства. Исследованиями установлено: а) только отсчеты 0; 0,5; и 1,0 наименьшего деления шкалы оцениваются с высокой точностью и постоянством, б) за погрешность отсчета может быть принята половина цены наименьшего деления шкалы. Так, например, секундомер имеет наименьшее деление шкалы 0,2 с; точный отсчет десятых долей этого деления невозможен из-за конечной толщины стрелки; систематическую погрешность можно принять равной 0.1с.

В лабораторной практике часто встречаются систематические погрешности, обусловленные свойствами измеряемого объекта, например, отклонениями от формы поверхности (неплоскостность, некруглость и т.д.) измеряемой детали, неоднородностью материала и т.п. Они могут быть переведены в случайные погрешности путем многократных измерений в различающихся условиях ( в различных местах, сечениях). Такой прием превращения систематической ошибки в случайную называется рандомизацией. Метод позволяет практически исключить многие неизвестные систематические погрешности и широко используется на практике. В заключение отметим, что никогда не следует ограничиваться однократным измерением. Всегда нужно проводить повторное кон­трольное измерение. Если результаты совпадает, на этом можно остановиться и за ошибку принять приборную погрешность Δ_пр, когда она неизвестна - половину цены наименьшего деления шкалы. При ответственных измерениях необходимо предварительно отградуировать прибор.

Если результаты измерений различаются, то следует предпринять целую серию повторных измерений с тем, чтобы вклад случайных погрешностей в общую ошибку стал меньше той, которую дает прибор.

Равноправный учет влияния систематических и случайных погрешностей на результат измерения будет дан ниже после ознакомления с теорией случайных ошибок.

Основные понятия теории вероятностей

Теория вероятностей изучает закономерности, присущие событиям массового характера.

Случайным называют событие, наступление которого нельзя достоверно предвидеть. В одних и тех же доступных наблюдению условиях оно может произойти или не произойти.

В основе теории вероятностей лежит закон больших чисел (теорема Чебышева), утверждающий, что при достаточно большом числе случайных событий их средний результат теряет свою случайность и может быть предсказан с достаточной точностью.

Закономерности, которым подчиняются массовые случайнее явления, называются статистическими, они имеют объективный

- 9 -

Характер, присущий всем явлениям внешнего мира.

Количественной оценкой возможности осуществления случайного события является его вероятность. Согласно классическому определению, вероятностью Р (А) некоторого события А называемся отношение числа случаев m, благоприятствующих его появлению к полному числу равновозможных случаев n , т.е.

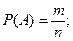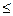m n (6)

Например, пусть бросается кубик, грани которого занумерованы числами 1,2,3,4,5,6. Какова вероятность выпадения номера 2? Из соображения симметрии следует, что n=6, а m=I. Следовательно, вероятность события Р (2) =1/6.

Существует другой способ оценки вероятности случайного события - оценка при помощи опыта. Основной характеристикой случайного события является относительная частота 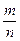его появления в определенных условиях, т.е. отношение числа m случаев, при которых данное событие произошло, к общему числу n наблюдений (возможных случаев), если последнее достаточно велико. Опыт показывает, что частота появления случайного события является более или менее устойчивой при различных сериях наблюдений. Например, при одном бросании кубика (единичное событие) выпадение определенного числа (2) будет событием случайным. Однако если опыт повторить много раз и учесть общее число бросаний n и число выпадений номера (2) (m). то относительная частота появления этого события 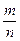будет близка к 1/6, т.е. .

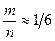Согласно статистическому определению, вероятностью события А называется предел, к которому стремится относительная частота при неограниченном увеличении числа испытаний

(7)

Вероятность произвольного события заключается между нулем и единицей .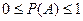

---

Дата добавления: 2014-10-31; просмотров: 10; Нарушение авторских прав

---

⇐ Предыдущая12345678910Следующая ⇒