
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценки точности измерений
По форме числового выражения различают абсолютные и относительные ошибки.
Абсолютная ошибка измерения - это ошибка, выраженная в единицах измеряемой величины. Количественно она определяется разностью между подученным при измерении значением величины Xi и ее истинным значением X0:
 . (1)
. (1)
Чем меньше погрешность измерения, тем оно точнее.
Отношение ошибки измерения к истинному значению измеряемой величины (если последняя не равна нулю) называется относительной ошибкой измерения:
 или
или  (2)
(2)
Она является величиной безразмерной, показывает, какую долю измеряемой величины составляет ошибка и обычно выражается в процентах.
Указание относительных ошибок приобретает особое значе-ние оттого, что позволяет сравнивать качество измерений величин разных наименований и порядков. Например, по относительным погрешностям можно сопоставлять точность измерения массы и длины, размеров микро- и макрообъектов.
Под точностью измерения понимают качество измерения, отражающее близость результата к истинному значению измеряемой величины. Точность измерения количественно характеризуется числом, равным обратному значению относительной погрешности, выраженной в долях измеряемой величины. Например, если погрешность измерения составляет ε=2·10-5, то точность этого измерения будет 5·104.
Результат измерения модно было бы записать в виде

однако истинная ошибка 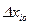 нам неизвестна, так как неиз -вестно истинное значение измеряемой величины Хо.
нам неизвестна, так как неиз -вестно истинное значение измеряемой величины Хо.
Поэтому обычно производят несколько (n раз) измерений искомой величины, и в качестве результата наиболее близкого к хо принимают их среднее арифметическое
 . (3)
. (3)
Под истинным значением измеряемой величины подразумевают
 (4)
(4)
Теория ошибок по результатам отдельных измерений позволяет вычислить пределы ±  вблизи
вблизи 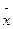 , внутри которых может находиться
, внутри которых может находиться  - с любой заданной вероятностью δ. Результат измерения представляют в форме
- с любой заданной вероятностью δ. Результат измерения представляют в форме
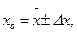
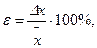 при
при 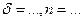 . (5)
. (5)
Эта запись означает, что истинное значение  с вероятностью
с вероятностью  находится внутри доверительного интервала
находится внутри доверительного интервала 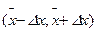
Дата добавления: 2014-10-31; просмотров: 263; Мы поможем в написании вашей работы!; Нарушение авторских прав |