Графическое представление результатов измерений

Для наглядного представления взаимной связи физических величин и их закономерного изменения результата наблюдений представляют графически.

Чаще всего используют прямоугольную систему координат. По оси абсцисс в произвольном масштабе откладывают независимую переменную, т.е. величину, значения которой задает сам экспериментатор. а по оси ординат ту величину, которую он при этом определяет. При выборе масштаба нужно исходить из следующих соображений: I) экспериментальные точки не должны сливаться друг с другом, т.е. они должны располагаться с разумным интервалом; 2) масштаб должен быть удобным. Проще всего, если I см соответствует 1,2,5,10,100,0.1 и т.д. единицам измеренной величины.

На осях координат следует указывать название или символ величины. Обязательно нужно также указывать единицы измерений, причем десятичный множитель следует отнести к единице измерения. Тогда деления на графике можно помечать цифрами 1,2,3... или 10,20.30 ..., а не 10000, 20000 ... и т.д. или 0.0001, 0,0002 и т.д. Экспериментальные данные следует отмечать "жирными", хорошо выделяющимися точками. По полученным на плоскости точкам проводят "наилучшую " плавную (неломаную) кривую (рис-6), которая может проходить не через все отмеченные точки, а близко к ним. Такая кривая дает нам возможность проводить графическим путем интерполяцию, т.е. находить значения У даже для таких значений X, которые непосредственно не наблюдались.

Если полученные данные не образуют прямой на линейной (миллиметровой) графической бумаге, то можно попытаться построить график в логарифмических координатах (или наносить логарифмы значений Х и У на линейную графическую бумагу). В логарифмических координатах график простой, но важной функции

(62)

имеет вид прямой. Переходя к логарифмам, действительно, получаем уравнение прямой:

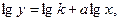
где К и а - постоянные.

Имеется также третий тип графической бумаги -полулогарифмическая, когда одна шкала является лога-рифмической, а другая -линейной. В этом случае получается прямая, если данные подчиняются закону

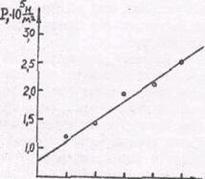Рис.6

(64)

После преобразований этой функции имеем

(65)

Чтобы получилась прямая, шкала по оси У должна быть логарифмической, а по оси х – линейной.