
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 6. Абсолютные и относительные величины
Абсолютные величины – статистические показатели, выражающие размеры (объемы, уровни) конкретных общественных явлений в единице веса, площади, объема и т.д., всегда являются именованными числами (имеют размерность).
При определении абсолютных величин используются различные методы измерения:
1. натуральный
2. условно – натуральный
3. трудовой
4. стоимостной (денежный).
При натуральном методе выражают размер явления в физических единицах (кг, л, м, ц), в некоторых случаях используют условно – натуральные единицы измерения, при этом имея ряд разновидностей одной и той же потребительной стоимости, одну из них принимают за единицу, а другие пересчитывают с помощью коэффициентов.
Трудовые единицы измерения (чел/час, чел/дни) используются для измерения трудовых показателей, трудоемкости, отработанного времени и др.
Стоимостной метод измерения используется для выражения объема продукции, прибыли, затрат.
Абсолютные величины бывают индивидуальными и общими (суммарными).
Индивидуальные абсолютные величины – показатели, которые выражают размеры количественных признаков у отдельных единиц совокупности.
Общие абсолютные величины – выражают величину того или иного признака у всех единиц совокупности. Их получают путем суммирования индивидуальных абсолютных величин.
При исследовании общественных явлений используют не только абсолютные, но и относительные величины.
Относительные величины– представляют собой частное от деления двух статистических величин и характеризуют количественное соотношение между ними.
При расчете относительной величины следует иметь ввиду, что в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе – показатель, с которым производится сравнение, принимаемый за основание или базу сравнения.
При получении относительных величин могут сопоставляться одноименные и разноименные величины. При сопоставлении одноименных величин получают простое кратное соотношение, которое выражается в форме коэффициента. При сопоставлении разноименных абсолютных величин получаем именованную относительную величину.
При решении задач по этой теме важно правильно определять виды относительных величин, понимать их экономический смысл, применять их в практической деятельности.
Введем условные обозначения:
Отчетный период – «1»;
Базисный (предшествующий) период – «0»;
Плановый период – «пл»
Виды относительных величин:
1. Относительная величина динамики (ОВД) – величина отражает изменение статистических показателей во времени.

Пример. Общая сумма месячного дохода работника в 2010 году составила 14564 руб., а в 2009 году – 13546. Чему равна относительная величина динамики? (14564 / 13546 = 1,075 или 107,5%) Следовательно, в 2010 году месячный доход работника увеличился по сравнению с 2009 годом на 7,5%.
При наличии данных за несколько периодов времени сравнение каждого данного уровня может производиться либо с уровнем предшествующего периода (цепной способ), либо с каким-то другим, принятым за базу сравнения (базисный способ). Таким образом, в зависимости оттого, что является базой сравнения, относительная величина динамики может быть рассчитана цепным или базисным способом.
Пример. Имеются данные о численности работников предприятия за 6 лет.
| Годы | Численность работников | Относительная величина динамики, % | |
| Базисный способ | Цепной способ | ||
| - | |||
| 106,2 | 106,2 | ||
| 97,1 | 91,4 | ||
| 87,3 | 89,9 | ||
| 76,4 | 87,5 | ||
| 116,7 | 152,6 |
Из приведенного примера видно, что цепной темп роста (цепной способ) характеризует изменение показателя за один какой-либо определенный отрезок времени, например за год, как в рассматриваемом примере, а базисный – за ряд лет, например за два, три года и т.д.
Последовательное перемножение цепных относительных величин дает возможность получить соответствующую базисную относительную величину (1,062*0,914=0,971).
2. Относительная величина планового задания (ОВпл.з.) отражает отношение планового показателя к предыдущему фактическому уровню.

Пример. Общая сумма месячного дохода работника в 2009 году составила 13546 руб., а в 2010 году планировалось ее увеличение до 13950 руб. Чему равна относительная величина планового задания? (13950 / 13546 =1,03 или 103%) Таким образом, планировалось увеличить месячный доход работника в 2010 году на 3%.
3. Относительная величина выполнения плана (ОВв.пл.) рассчитывается как отношение фактического уровня к плановому.

Пример. В 2010 году планировалось увеличение месячного дохода работника до 13950 руб., а фактически его величина составила 14564 руб. Чему равна относительная величина выполнения плана. (14564 / 13950 =1,044 или 104,4%) Вывод: месячный доход работника увеличился в 2010 году по сравнению с планом на 4,4%.
Между относительной величиной динамики, относительной величиной планового задания и выполнения плана существует взаимосвязь:
ОВД = ОВпл.з. * ОВв.пл.
4. Относительная величина структуры (ОВС) – это отношение части к целому.
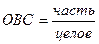 Показывает, какой долей обладает i-ая часть в общем итоге.
Показывает, какой долей обладает i-ая часть в общем итоге.
Характеризует удельный вес (или долю) отдельных частей, из которых состоит целое. Она может называться удельным весом - если целое принято за 100%. Если целое принято за 1, то – доля.
Пример. Имеются данные о группировке промышленных предприятий по численности работников:
| Группы предприятий по численности работников, чел. | Число предприятий, ед. | Удельный вес предприятий, % | Алгоритм расчета |
| до 200 | 50,6 | 253/500*100 | |
| 201 – 500 | 25,2 | 126/500*100 | |
| 501 – 1000 | 16,8 | 84/500*100 | |
| свыше 1000 | 7,4 | 37/500*100 | |
| итого |
Вывод: наибольший удельный вес – 50,6% составляют предприятия с численностью до 200 человек.
5. Относительная величина координации (ОВК) – это соотношение частей целого между собой. Результат показывает во сколько раз сравниваемая часть больше или меньше части, принятой за основание.
Пример. На начало исследуемого периода в регионе было 50 высших учебных заведений, а общеобразовательных школ – 4000. Сколько школ приходится на каждые 10 вузов? (4000 / 50 * 10 = 800) Вывод: на каждые 10 вузов приходится 800 школ.
Пример. Численность экономически активного населения страны составила 72772 тыс. чел., в том числе занятые в реальном секторе экономике – 64639 тыс. чел., безработные составили 8133. Сколько человек занятого населения приходится на одного безработного (64639/8133 = 8 чел.) Вывод: на 1 безработного, приходится 8 человек работающего населения.
6. Относительная величина интенсивности (ОВИ) характеризует степень распространения явления в присущей ему среде.

Этот показатель исчисляется, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Может выражаться как в процентах, так и именованной величиной.
Пример. На конец исследуемого периода численность врачей всех специальностей составляла 1104,3 тыс. человек, а численность населения 285,8 млн. чел. Сколько врачей приходится на каждый 10000 жителей (1104,3 / 285800 * 10000 = 38) Вывод: на каждые 10000 жителей приходится 38 врачей.
К относительной величине интенсивности относятся такие экономические показатели, как фондоотдача (f=Q/ОПФ), выработка (w=Q/Ч), материалоотдача (Mo=Q/МЗ).
7. Разновидностью относительной величины интенсивности является уровень экономического развития. Уровень экономического развития показывает, сколько продукции приходится на душу населения.
8. Относительная величина сравнения – это соотношение одноименных показателей, относящихся к разным объектам или разным территориям, и взятых, как правило, за одно и тоже время.
Пример. Выпуск цемента в России и в США за год.
Дата добавления: 2015-02-10; просмотров: 678; Мы поможем в написании вашей работы!; Нарушение авторских прав |