Повторно вычисляем остатки и фактически возвращаемся к этапу 3

2) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки;

2. вычисляем остатки

3. оцениваем адекватность и точность модели;

3) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки;

2. вычисляем остатки

3. находим d-критерий

4. используя d-критерий определяем наличие автокорреляции

5. находим оценку коэффициента автокорреляции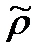

6. используя данную оценку 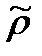находим уравнение, где автокорреляция устранена

7. проводим определение параметров полученного уравнения и находим новые значения оценок

8. повторно вычисляем остатки и фактически возвращаемся к этапу 3.

42. Метод Хилдрета-Лу, используемый для оценки коэффициента автокорреляции случайного члена уравнения регрессии и коэффициентов самого уравнения регрессии, заключается в следующем:

1) В данном методе используется итерационная процедура. Находятся оценки факториальных переменных уравнения, далее вычисляются остатки, находится оценка коэффициента автокорреляции из авторегрессионной схемы I порядка, далее, используя данную оценку , находится уравнение, в котором полностью устранена автокорреляция, производим определение параметров этого уравнения, повторно вычисляются остатки и возвращаемся к этапу 3. Процесс повторяется до того пока не будет получена требуемая точность.

2) В данном методе исследователь задает интервал изменения величины и шаг. Для каждого значения производится оценка фактических параметров из уравнения, в котором автокорреляция полностью устранена. Затем выбирается из полученных результатов такой, который дает min стандартную ошибку для преобразования уравнения. Используемые в этом уравнении значения и факториальные переменные принимаются за искомые.

3) В данном методе исследователь исключает один из факторов уравнения регрессии, который, по мнению исследователей, считается менее значимым, или имеет менее высокий коэффициент корреляции с результирующим фактором, или имеет более высокий коэффициент корреляции с другими факторами.

43. Какие системы алгебраических уравнений называются системами одновременных уравнений?

1) Уравнения, в которых одни переменные являются только объясняющими для всех уравнений, а другие переменные являются только результирующими переменными для всех уравнений.

2) Уравнения, в которых все переменные являются либо только объясняющими переменными, либо только результирующими переменными.

3) Уравнения, в которых одни и те же переменные в различных уравнениях используются как объясняющие переменные, так и результирующие переменные.

44. Почему нельзя определить параметры уравнения функции потребления простой кейнсианской модели формирования доходов?