БАҚЫЛАУ ЖҰМЫСЫ №1.

Тақырыбы: «ВЕКТОРЛЫҚ АЛГЕБРА».

Мақсаты: және нүктелерінің координаттары белгілі болса, векторының координаттарын, оның ұзындығын табуды үйрену, себебі аналитикалық геометрияның көптеген есептері векторлардың көмегімен шығарылады, сол сияқты векторлардың скаляр, векторлық, аралас көбейтінділерін таба білу.

Тапсырма:

ABCD пирамида төбелері берілген

а/ 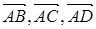векторларының ұзындығын және орт тар бойынша жіктеуін жазыңыз.

б/ векторларының арасындағы бұрышты табыңыз.

в/ 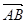векторынан векторының проекциясын табыңыз.

г/ ABC жағының S ауданын табыңыз.

д/ ABCD пирамиданың V көлемін табыңыз.

е/ Суретін сал.

1/

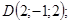
2/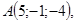

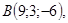
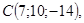
3/

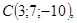
4/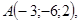

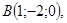
5/

6/

7/

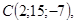
8/

9/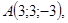

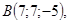
10/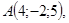

11/

12/

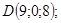
13/

14/

15/

16/

17/

18/

19/

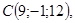
20/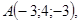

БАҚЫЛАУ ЖҰМЫСЫ №2.

Тақырыбы: «ВЕКТОРЛЫҚ АЛГЕБРА ЖӘНЕ АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ»

Мақсаты: Түзудегі, жазықтықтағы, кеңістіктегі базисті анықтау білу. Түзудің және жазықтықтың әр түрлі теңдеулерін құрастыра білу.

Тапсырма:

Берілді: А, В, С, А нүктелердің координаттары

а) 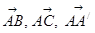векторларын жүйесінде жазыңыз, осы векторлардың модулдарын табыңыз.

б)АВСD – АВСD 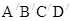параллелепипедтің табаны болатындай етіп, D(х,у,z) нүктесінің координаттарын табыңыз. векторын құрастырыңыз.

в) 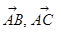векторлары жазықтықта базис құрай ма, тексеріңіз

г) 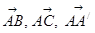векторлары кеңістікте базис құрай ма, тексеріңіз.

д)АВСD параллелограмның ауданын табыңыз.

е) 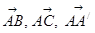векторларына салынған парпллелепипедтің көлемін табыңыз.

ж)Табыңыз: cos ; .

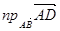з) АВСD жазықтықтың теңдеуін жазыңыз.

и) А нүктесінен параллелепипедтің табанына А N перпендикуляр түзудің теңдеуін жазыңыз.

к) N нүктесінің координатасын және 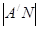қашықтықты табыңыз.

л) Параллелепипед салыңыз.

1. A (2, 0, 0), B (0, 2, 0), C (0, 0, 2), A^/ (0, 0, 6)

2. A (3, 0, 0), B (0, 3, 0), C (0, 0, 3), A^/ (0, 0, 6)

3. A (-2, 0, 0), B (0, 2, 0), C (0, 0, 2), A^/ (0, 0, 6)

4. A (-3, 0, 0), B (0, 3, 0), C (0, 0, 3), A^/ (0, 0, 8)

5. A (2, 2, 0), B (0, 2, 2), C (2, 0, 2), A^/ (0, 0, 8)

6. A (2, -2, 0), B (0, 2, 2), C (0,-2, 2), A^/ (0, 0, 8)

7. A (3, -3, 0), B (0, 0, 3), C (0,-3, 0), A^/ (0, 0, 9)

8. A (4, -4, 0), B (0, 4, 4), C (6,-4, 4), A^/ (0, 0,-4)

9. A (2, -2, 0), B (0, -2, 2), C (-2, 0, 0), A^/ (0, 0, 4)

10. A (3, -3, 0), B (0, 3, 3), C (-3, 0, 0), A^/ (0, 0, 5)

11. A (4, -4, 0), (B 0, -4, 4), C (-4, 0, 0), A^/ (0, 0, 6)

12. A (5, -5, 0), B (0, -5, 5), C (-5, 0, 0), A^/ (0, 0, 7)

13. A (0, 0, 3), B (0, -3, 4), C (-3, 0, 0), A^/ (0, 0, 5)

14. A (0, 0, 4), B (0, -4, 5), C (-4, 0, 0), A^/ (0, 0, 6)

15. A (0, 0, -3), B (0, 3, 0), C (0, 0, 3), A^/ (-3, 3, 5)

16. A (3, -5, 0), B (0, -3, 3), C (3, 0, 0), A^/ (-3,-3, 5)

17. A (3, -5, 0), B (0, -3, 3), C (0, 0, 3), A^/ (0, 0, 6)

18. A (1, -1, 0), B (0, 1, 1), C (0, -1, 1), A^/ (0, 0, 5)

19. A (-5, 0, 0), B (0, 5, 0), C (0, 0, 5), A^/ (0, 0, 7)

20. A (0, 1, 0), B (2, 1, 0), C (3, 0, 0), A^/ (0, 0,-4)

21. A (1, 3, 1), B (-1, 6, 1), C (-1, 3, 7), A^/ (1, 6, 9)

22. A (1, 2, 2), B (-1, 5, 2), C (-1, 2, 8), A^/ (1, 5, 10)

23. A (2, 3, 1), B (0, 6, 1), C (0, 3, 7), A^/ (2, 6, 9)

24. A (2, 2, 2), B (0, 5, 2), C (0, 2, 8), A^/ (2, 5,10)

25. A (1, 3, 2), B (-1, 6, 2), C (-1, 3, 8), A^/ (1, 6, 10)