ЖЕКЕ ТАПСЫРМА №6

Тақырыбы: «БІРНЕШЕ АЙНЫМАЛЫЛЫ ФУНКЦИЯ».

Мақсаты: Көп айнымалылы функциялардың толық зерттеуін еркін жүргізу, бірінші және екінші ретті дербес туындыларды, аралас туындыларды таба білу

Тапсырма:

1. Дербес туындылар және бірінші ретті толық дифференциал

2. Барлық дербес туындылар және екінші ретті толық дифференциал

3. Теңдеулер жүйесін шешу арқылы стационар нүктелерін:

,

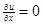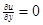
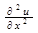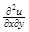4. Әрбір стационар нүктелері үшін дискриминант құрастырыңыз ∆=АС-В², мұндағы А= , В= , С=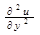

5. Егер бар болса, функцияның экстремумын және экстремум нүктесіндегі функцияның мәнін

6. М нүктесіндегі функцияның градиент шамасы және бағытын

1. u =х²-2х+1+2у², М(1;1)

2. u=е^х-у(х²-2ху +2у²), М(1;1)

3. u=х²+ху+ у²-2х-у, М(1;1)

4. u=6х³у²-х⁴у²- х³у³, М(1;1)

5. u=х⁴+ у⁴+4ху-2у²-2х², М(1;1)

6. u=(х²+2у²)е^-(х+у),М(1;1)

7. u=1-(х²+у²)^2/3, М(1;1)

8. u=(х²+у²)е^-(х+у), М(1;1)

9. u=(1+х-у)/√1+х²+у², М(1;1)

10. u=8/х+х/у+у, М(1;1)

11. u=е^х-у(х²-2у²), М(1;1)

12. u =х³+3ху²-15х-12у, М(1;1)

13. u=3х+6у-х²-ху-у², М(1;1)

14. u=sinхsinу, М(П/4; П/4)

15. u= х³-2у³-3х+6у, М(0;0)

16. u=хуLn(х²+у²) , М(e/√2; e/√2)

17. u =е^х+2у(х²-у²), М(-4/3;2/3)

18. u =1/2х²-4ху+9у²+3х-14у+1/2, М(2;1)

19. u =х²-ху+у², М(1;1)

20. u =х³+у³-х²-2ху-у², М(1;1)

21. u =(х-2у)е^-(х+у), М(0;0)

22. u =х/у+1/х+у, М(2;1)

23. u =4х³+3х²у+3ху²-у³, М(1;1)

24. u =х²-2х-2у²-1, М(1;1)

25. u =х²+у²-2х-4√ху-2у+8,М(1;1)

26. u =2х³-ху²+5х²+у², М(0;1)

27. u =3х²-2х√у+у-8х+8, М(1;4)

28. u =уLnх, М(e; e)

29. u =х²-ху-у², М(1;1)

30. u =х³-2х²у²+у⁴, М(1;1)

31. u =sinх+sinу+sin(х+у), М(0;0)

32. u =ху+1/(2(х+у)), М(1;0)

33. u =х²-2ху+2у²+2х, М(1;1)

34. u =ху√1 -х²/ а²- у²/в², М (1;0)