
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные законы и формулы. 1. Материальная точка – это твёрдое тело, размерами которого в данной задаче можно пренебречь.
1. Материальная точка – это твёрдое тело, размерами которого в данной задаче можно пренебречь.
Радиус-вектор 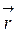 – это вектор, определяющий положение материальной точки в любой момент времени в заданной системе отсчёта
– это вектор, определяющий положение материальной точки в любой момент времени в заданной системе отсчёта
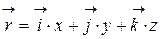 ,
,
где  единичные векторы направлений; x, y, z – координаты точек.
единичные векторы направлений; x, y, z – координаты точек.
2. Основная задача кинематики поступательного движения заключается в нахождении явного вида функции 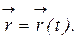
3.Вектор средней скорости материальной точки
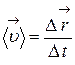 ,
,
где 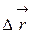 – перемещение материальной точки за интервал времени
– перемещение материальной точки за интервал времени 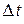 .
.
Модуль средней скорости
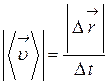 .
.
4. Средняя путевая скорость ( скалярная величина)
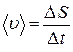 ,
,
где 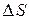 – путь, пройденный точкой за время
– путь, пройденный точкой за время 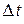 .
.
5. Вектор мгновенной скорости материальной точки
 .
.
Модуль мгновенной скорости
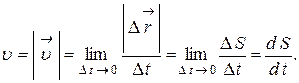
Вектор 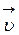 можно разложить на составляющие, направленные вдоль координатных осей
можно разложить на составляющие, направленные вдоль координатных осей

 ,
,
где  ;
; 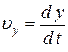 ;
; 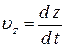 – проекции вектора скорости на оси координат.
– проекции вектора скорости на оси координат.
Модуль мгновенной скорости через проекции
 .
.
6. Вектор среднего ускорения материальной точки
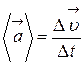 ,
,
где 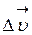 – изменение вектора скорости за интервал времени
– изменение вектора скорости за интервал времени 
7. Вектор мгновенного ускорения материальной точки

Вектор 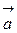 можно разложить на составляющие, направленные вдоль координатных осей
можно разложить на составляющие, направленные вдоль координатных осей
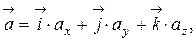
где 
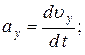
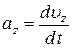 – проекции вектора ускорения на оси координат.
– проекции вектора ускорения на оси координат.
Модуль мгновенного ускорения через проекции
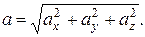
8. В случае криволинейного движения ускорение 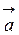 равно геометрической сумме тангенциальной
равно геометрической сумме тангенциальной 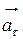 и нормальной
и нормальной 
составляющих (рис.1)
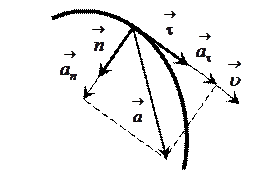 |
Рис. 1
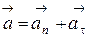 ,
,
где 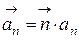 ;
; 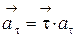 .
.
Модули этих ускорений 
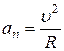 ;
; 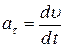 ;
; 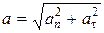 ,
,
где R – радиус кривизны траектории; 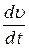 – производная модуля скорости по времени.
– производная модуля скорости по времени.
9. Основная задача кинематики вращательного движения заключается в нахождении явного вида функции 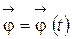 ,
,
где  – угловое перемещение материальной точки, модуль которого равен углу поворота.
– угловое перемещение материальной точки, модуль которого равен углу поворота.
10. Вектор средней угловой скорости

где 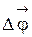 – приращение угла поворота за промежуток времени
– приращение угла поворота за промежуток времени  .
.
11. Вектор мгновенной угловой скорости
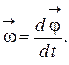
Направление векторов  и
и  определяют по правилу правого винта (
определяют по правилу правого винта (  и
и  – псевдовектора, направленные вдоль оси вращения), (рис. 2)
– псевдовектора, направленные вдоль оси вращения), (рис. 2)

Рис. 2
12. Вектор среднего углового ускорения
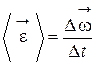 .
.
13. Вектор мгновенного углового ускорения
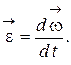
14. Связь между линейными и угловыми величинами:
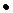 путь, пройденный точкой
путь, пройденный точкой 
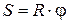 ,
,
где R – расстояние от оси вращения до точки;
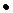 скорость точки
скорость точки
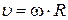 ;
;
 тангенциальная составляющая ускорения точки
тангенциальная составляющая ускорения точки
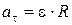 ;
;
 нормальная составляющая ускорения точки
нормальная составляющая ускорения точки
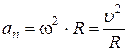 .
.
15. Период вращения T при 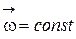 – это время, за которое точка совершает один оборот, то есть поворачивается на угол
– это время, за которое точка совершает один оборот, то есть поворачивается на угол 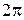
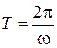
или
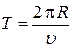 .
.
16. Частота вращения n – число полных оборотов в единицу времени
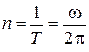 .
.
Тогда
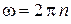 .
.
Таблица 1
Основные уравнения кинематики поступательного и вращательного движений
| Движение | Поступательное | Вращательное |
| равномерное |  ; ; 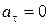 а)
а) 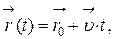 где
где 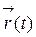 – радиус-вектор, определяющий положение материальной точки в момент времени t; – радиус-вектор, определяющий положение материальной точки в момент времени t;
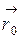 – радиус-вектор, определяющий положение материальной точки в момент времени t=0.
б)в координатной форме – радиус-вектор, определяющий положение материальной точки в момент времени t=0.
б)в координатной форме
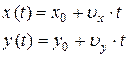
| 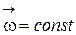 ; ;  а)
а) 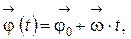 где
где  – начальное угловое перемещение.
б) в проекции на ось вращения Z – начальное угловое перемещение.
б) в проекции на ось вращения Z
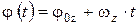 . .
|
| равноускоренное |  а)
а)  где
где 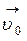 – начальная скорость.
б)в координатной форме – начальная скорость.
б)в координатной форме
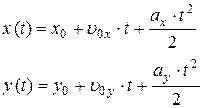 в)
в)  г) в координатной форме
г) в координатной форме
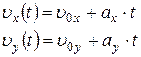
|  а)
а) 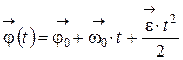 ,
где ,
где 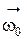 – начальная угловая скорость.
б) в проекции на ось вращения Z – начальная угловая скорость.
б) в проекции на ось вращения Z
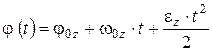
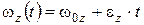 . .
|
Дата добавления: 2015-02-10; просмотров: 225; Мы поможем в написании вашей работы!; Нарушение авторских прав |