И абсолютно твердого тела.

Кинематика движения материальной точки

Кинематика – раздел механики, изучающий движение тел без анализа причин, обусловливающих это движение. Простейшей моделью физического тела является материальная точка (МТ), которой называют тело, размерами которого можно пренебречь в условиях данной задачи.

положение любого тела в пространстве может быть определено только по отношению к системе отсчета (СО). Для количественного описания движения с последней связывается система координат, в простейшем случае – декартова прямоугольная система координат.

Положение мт в такой системе задается радиус-вектором, проведенным из начала координат к данной точке:

r =x×e_x + y×e_y + z×e_z. (1.1)

· Вектор Dr, соединяющий начальную и конечную точки движения, называется перемещением. Линия, которую описывает МТ при своем движении, представляет собой траекторию. Она задается уравнением кривой. Путь s – это длина участка траектории, причем всегда .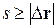

· Мгновенная скорость МТ есть первая производная радиус-вектора по времени. В декартовой системе координат:

V = = = V_x×e_x + V_y×e_y + V_z×e_z , (1.2)

где ; ; .

Модуль вектора скорости характеризует изменение пройденного пути со временем:

. (1.3)

Зная мгновенную скорость как функцию времени, можно найти вектор перемещения МТ:

Dr = 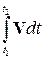, (1.4)

а также изменение координат и пройденный путь:

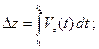
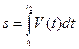; . (1.5)

· Мгновенным ускорением называется первая производная скорости по времени:

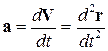, (1.6)

где .

Зная функцию 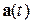, можно определить изменение вектора скорости за промежуток времени междумоментами t₁ и t₂:

. (1.7)

Если известны начальные положение r(0), скорость МТ V(0) и функция 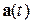, то

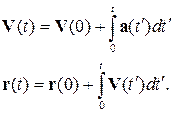(1.8)

Вектор ускорения в общем случае составляет некоторый угол с касательной к траектории в данной точке. Часто оказывается удобным разложить вектор a на две составляющие: касательную к траектории в данной точке – a_t и перпендику-лярную к касательной – a_n:

a = a_t + a_n.

Величины a_t иa_n называют тангенциальным и нормальным ускорениями соответственно.

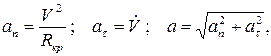(1.9)

где R_кр – радиус кривизны траектории.

· При описании криволинейного движения материальной точки удобно пользоваться угловыми характеристиками движения – угловыми перемещением, скоростью и ускорением.

Малым угловым перемещением МТ Da называют вектор, равный по величине углу поворота радиуса, проведенного от оси вращения к этой точке, и направленный вдоль указанной оси по правилу правого винта.

Угловая скорость есть первая производная по времени углового перемещения:

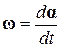. (1.10)

При движении МТ по окружности связь между линейной и угловой скоростью определяется соотношением:

V = [ω,r] . (1.11)

Угловым ускорением называют первую производную по времени от вектора угловой скорости:

. (1.12)

Если движение происходит в одной плоскости, то можно определить скалярную величину – угол поворота радиус-вектора МТ:

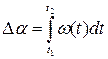. (1.13)

· Положение твёрдого тела (ТТ) в пространстве полностью определяется заданием координат трех не совпадающих друг с другом точек, то есть заданием положения треугольника.

Простейшим типом движения ТТ является поступательное. При этом каждая прямая, связанная жестко с ТТ, движется параллельно самой себе. При описании такого движения, когда все точки тела движутся по одинаковым траекториям, можно пользоваться соотношениями, определяющими кинематику материальной точки.

Другим простейшим видом представляется вращение ТТ около неподвижной оси. Описать такое движение можно всего лишь одной координатой, задав угол поворота ТТ относительно фиксированного направления.

· Более сложным оказывается так называемое плоское движение ТТ, при котором все его точки движутся в параллельных плоскостях. Такое движение можно представить, комбинируя поступательное движение тела и его поворот вокруг оси перпендикулярной плоскостям, в которых движутся точки ТТ. Тогда скорости точек тела:

, (1.14)