Физический смысл имеет только одно решение, соответствующее t1 > t, т.е. .

Искомая дальность полёта находится из условия:

.

Задача

1.2.Точка А находится на ободе колеса радиуса R, которое катится без проскальзывания с постоянной скоростью V₀ по горизонтальной плоскости. Найти скорость точки А, написать уравнение траектории (в параметрической форме), по которой движется точка А, и её путь за один оборот колеса.

Решение

Рассмотрение будем вести относительно системы отсчёта, связанной с Землей. Систему координат расположим, как это показано на рисунке. Движение обруча – плоское. В частности оно может быть представлено как совокупность поступательного перемещения со скорость движения оси колеса V₀ и вращения с угловой скоростью 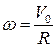относительно неё.

Координаты точки А:

Это уравнения циклоиды.

Компоненты скорости точки А:

Модуль скорости:

.

Время одного полного оборота колеса находится из условия:

V₀ ×T = 2pR, т.е. .

Путь, пройденный точкой А за период:

Движение колеса можно представить также как последова-тельность поворотов вокруг мгновенной оси О_М (так как проскаль-зывание отсутствует, то в любой момент времени скорость точки касания колеса и плоскости О_М равна нулю).

V_A=[wr_A],

V_А = = .

Естественно, что мы получили такой же результат.

Задача

1.3.* Зависимость модуля скорости частицы V от пройденного пути s определяется функцией V(s) = V₀ - bs.