Задачи для самостоятельного решения. 1.5. Атом в молекуле, совершая так называемые “маятниковые колебания”, движется по дуге окружности радиуса R по закону s = s0coswt (s – длина дуги)

1.5. 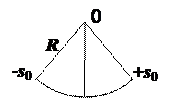Атом в молекуле, совершая так называемые “маятниковые колебания”, движется по дуге окружности радиуса R по закону s = s₀coswt (s – длина дуги). Найти полное ускорение атома в точках а) s = 0 и б) s = ±s₀. Считать R = 10^-7 см, s₀ = 10^-8 см и w = 10¹³ с^-1.

1.6.Частица движется по круговой орбите радиуса R так, что зависимость угла поворота радиус-вектора от времени имеет вид: j(t) = a + bt - ct². Найти зависимость от времени: 1) угловой скорости, 2) линейной скорости, 3) тангенциального ускорения, 4) нормального ускорения и 5) полного ускорения частицы.

1.7.Шар вращается вокруг оси, проходящей через его центр с помощью электромотора с частотой n = 1800 об/мин. После выключения электромотора шар, вращаясь равнозамедленно, совершил N = 150 оборотов и остановился. Сколько времени прошло с момента выключения до остановки.

1.8.Диск электропроигрывателя вращается с постоянной угловой скоростью, делая n = 33,(3) об/мин. После выключения двигателя диск останавливается за счет трения через t = 20 c. Считая движение равнозамедленным, найти, сколько оборотов сделает диск после выключения двигателя до полной остановки.

1.9.Маховик вращается, совершая n₀ = 20 об/с. После выключения двигателя, вращавшего маховик, он остановился, сделав N = 250 оборотов. Считая движение равнозамедленным, найти угловое ускорение маховика.

1.10.Радиус-вектор частицы определяется выражением r= 3t²×e_x + 4t²×e_y + 7×e_z (м). Вычислить а) путь s, пройденный частицей за первые 10 с движения, б) модуль перемещения |Δr| за это время, в) объяснить полученный результат.

1.11.Радиус-вектор частицы определяется выражением r= 3t²×e_x + 2t×e_y + 1×e_z (м). Найти: а) зависимость от времени скорости V и ускорения a частицы, б) модуль скорости в момент времени t = 1 c, в) приближённое значение пути, пройденного частицей за 11-ю секунду движения.

1.12.Точка движется ускоренно по окружности вокруг неподвижной оси. Указать направления векторов линейной и угловой скорости, а также линейного и углового ускорения.

1.13.Укажите на чертеже направления вектора линейного ускорения математического маятника в следующих случаях: а) в момент прохождения положения равновесия, б) в крайнем положении, в) в промежуточном положении. Какие силы создают ускорение в рассмотренных случаях?

1.14.Указать на чертеже направление углового ускорения в следующих случаях: а) диск вращается вокруг собственной неподвижной оси с возрастающей угловой скоростью, б) направление оси вращения поворачивается, а скорость вращения диска остается неизменной.

1.15.Точка совершает гармонические колебания вдоль оси X с амплитудой А = 4 см и частотой n = 5 Гц. Найти проекции скорости V_x и ускорения a_x точки в тот момент, когда ее смещение от положения равновесия определено координатой x₁ = 2 см.

1.16.Точка движется по окружности радиуса R = 20 см с постоянным тангенциальным ускорением a_t = 5 см/c². Через какое время после начала движения нормальное ускорение а_n будет: а) равно тангенциальному, б) вдвое больше тангенциального?

1.17.Компоненты скорости частицы изменяются со временем по законам: V_x = А×cosωt, V_y = А×sinωt и V_z = 0, где А и ω – константы. Найти модуль скорости частицы, модуль ускорения, а также угол между векторами скорости и ускорения. На основании получен-ных результатов сделать вывод о характере движения частицы.

1.18.Зависимость координат частицы от времени имеет вид: x = А×cosωt, y = А×sinωt и z = 0 (А и ω - константы). Определить радиус-вектор r, скорость V и ускорение ачастицы, а также их модули. Найти:

а) скалярное произведение векторов r и V; б) скалярное произведение векторов r и а.Что означают полученные результаты?

в) Записать уравнение траектории частицы.

г) В каком направлении движется по траектории частица?

д) Охарактеризовать движение частицы.

1.19.Модуль скорости частицы меняется по закону V = V₀e^-bt. Каков физический смысл константы b?

1.20.Материальная точка движется по прямой с начальной скоростью V₀ = 4 м/c, причем ускорение точки направлено в сторону, противоположную вектору V₀, и изменяется со временем по закону a = kt². Определить перемещение точки за первые t = 3 c движения и ее среднюю скорость за этот же промежуток времени. (k = 1 м/с⁴).

1.21.Цилиндрическое тело замедленно вращается в вязкой среде вокруг своей оси. При этом абсолютная величина углового ускорения прямо пропорциональна угловой скорости. Найти:

а) закон изменения угловой скорости и построить график ω = f(t), б) за какой промежуток времени угловая скорость уменьшится в n₁ = 6 раз, если известно, что в n₂ = 2 раза она уменьшается за время t₂ = 20 с. Начальная скорость вращения равна w₀.

1.22.Колесо вращается с постоянным угловым ускорением b = 2 рад/с². Через t = 0,5 с после начала движения полное ускорение точек обода колеса стало равно a = 13,6 см/с². Найти радиус колеса.

1.23. Цилиндр катится без скольжения со скоростью V₀ (см. рис.). Найти скорости точек 1, 2 и 3. Выразить их через орты координатных осей.

1.24.Найти ускорение точки 2 в условиях предыдущей задачи.

1.25.* На обод колеса, имеющего неподвижную горизонтальную ось, намотана нить, на конце которой подвешен груз. В некоторый момент груз начинает опускаться с постоянным ускорением а₀ и при этом приводит во вращение колесо. Найти полное ускорение точек обода колеса в зависимости от высоты h, на которую опускается груз. Радиус колеса R.

1.26.Лодка пересекает реку с постоянной относительно воды скоростью V, перпендикулярной к течению. Скорость течения реки, ширина которой d, рав­на нулю у берегов и линейно возрастает по мере приближения к середине реки, где достигает значения U₀ {т.е. U(y) = 2U₀y/d при 0  y < d/2 и U(y) = 2U₀ – 2U₀y/d при d/2  y < d}. Каков снос лодки DХ вниз по течению, от места ее отправления до причала на противопо­ложном берегу реки?