Полученные зависимости представлены графически на рисунке и имеют ясный физи-ческий смысл, который мы предлагаем продумать читателю самостоятельно.

Задача

1.4.* Лодка пересекает реку с постоянной относительно воды и перпендикулярной берегам скоростью V_отн = 0,3 м/с. Ширина реки равна H = 63 м. Скорость течения изменяется по параболическому закону , где y – расстояние от берега, u₀ – константа, равная 5 м/с. Найти снос лодки L вниз по течению от пункта ее отправления до места причаливания на противоположном берегу.

Решение

Как известно, механическое движение всегда носит относительный характер – его характеристики различны в разных системах отсчёта. Поскольку в задаче дана скорость лодки относительно воды, будем использовать две системы отсчёта – «неподвижную», связанную с берегом, и «движущуюся» – связанную с водой в реке. Направим координатные оси обеих систем отсчёта вдоль берега (OX) и перпендикулярно к нему (OY). Скорость лодки относительно неподвижной системы отсчёта равна сумме скорости лодки относительно движущейся системы отсчёта (воды) и скорости движущейся системы отсчёта относительно неподвижной (берега):

V = V_отн + u.

Сложное движение лодки можно представить как сумму двух более простых – вдоль берега и перпендикулярно к нему. Первое происходит со скоростью движения относительно воды V_отн, второе – со скоростью воды относительно берега u(y). Поскольку вдоль оси OY движение является равномерным закон этого движения можно записать в виде:

y(t) = V_отн×t. (1)

Это позволяет определить зависимость изменения скорости лодки вдоль оси OX от времени. Последнее необходимо для определения изменения координаты в каждом направлении, как интеграл соответствующих функций скорости по времени в пределах «времени переправы» t :

, (2)

. (3)

Интеграл в равенстве (2) легко вычисляется и, поскольку ширина реки H известна, это позволяет найти время переправы:

. (4)

Для определения сноса лодки вниз по течению L = x(t) придётся провести довольно кропотливую, но несложную процедуру вычисления соответствующих интегралов:

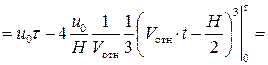
[подставим найденное ранее значение t = H/V_отн]

.

Итак, снос лодки с учётом численных данных задачи равен:

м.