Б) Определить зависимость V от t.

Решение

а) Заданную зависимость V от пройденного пути представим в виде:

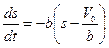. (1)

Соотношение (1) представляет собой дифференциальное уравнение первого порядка. Если провести замену переменной s(t)на 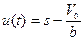, то, поскольку дифференциалы величин ds и du (малые приращения) не отличаются, равенство (1) принимает вид:

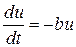. (2)

Это так называемое уравнение с разделяющимися переменными, решение которого после приведения к виду:

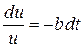. (3)

выполняется посредством интегрирования правой и левой частей:

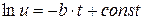. (4)

Константу интегрирования удобно представить как lnu₀, тогда после простых преобразований и потенциирования получим:

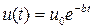. (5)

Возвращаясь к исходной переменной, запишем:

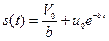. (6)

Константа интегрирования u₀, определяется из начальных условий – s(0) = 0:

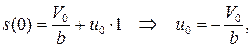
Итак, путь зависит от времени по закону:

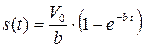. (8)

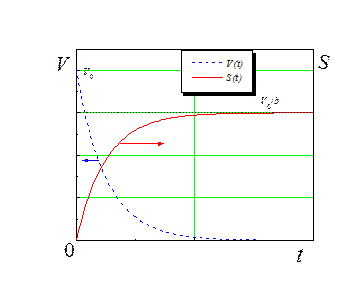б) Зависимость скорости от времени получим, диф-ференцируя равенство (8):

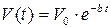. (9)