
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Системы линейных уравнений и неравенств с двумя неизвестными
Системой двух линейных уравнений с двумя неизвестными называют совокупность двух уравнений вида:
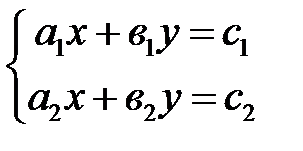 (2.1).
(2.1).
Решением системы (2.1) называют пару чисел 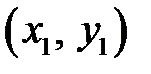 , удовлетворяющих каждому уравнению системы т.е.:
, удовлетворяющих каждому уравнению системы т.е.:
 .
.
Каждое уравнение системы определяет прямую на плоскости, следовательно, решение системы есть точка пересечения этих прямых. Найдем координаты этой точки. Выразим из первого уравнения системы неизвестное 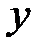 и подставим его во второе уравнение:
и подставим его во второе уравнение: 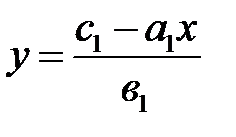 ;
; 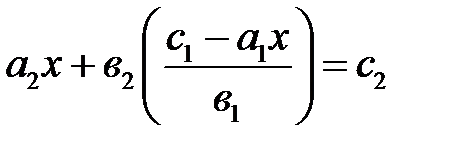 ;
; 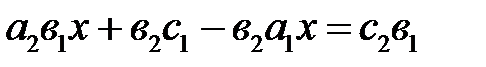 .
.
 .
.
Подставим значение 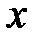 в выражение
в выражение 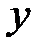 , получим:
, получим:  .
.
Введем обозначение: 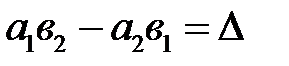 . Величину
. Величину  будем называть определителем второго порядка системы (2.1). Тогда
будем называть определителем второго порядка системы (2.1). Тогда  ,
,  будем называть вспомогательными определителями системы. Запишем определители в виде таблиц, состоящих из двух строк и двух столбцов:
будем называть вспомогательными определителями системы. Запишем определители в виде таблиц, состоящих из двух строк и двух столбцов:
 .
.
Как видно, определитель системы составлен из коэффициентов при неизвестных первого и второго уравнений. Определители  и
и 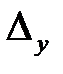 получены из определителя
получены из определителя  , путем замены первого и второго столбцов, соответственно, столбцом свободных членов системы, что и оправдывает обозначения
, путем замены первого и второго столбцов, соответственно, столбцом свободных членов системы, что и оправдывает обозначения  и
и 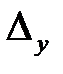 .
.
Очевидно, что решение системы (2.1) можно записать в виде: 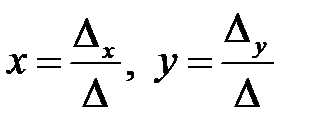 .
.
Пример 3. Решить систему:
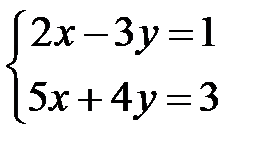 .
.
Решение. Вычислим определитель  :
:
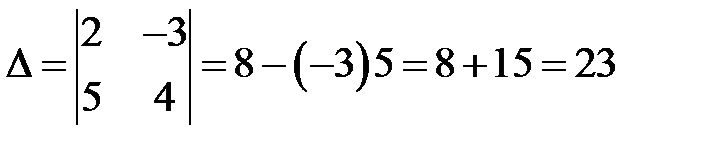 .
.
Определитель 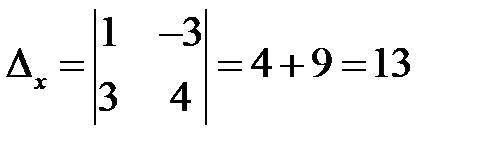 .
.
Определитель 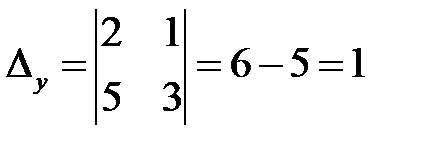 . Тогда:
. Тогда: 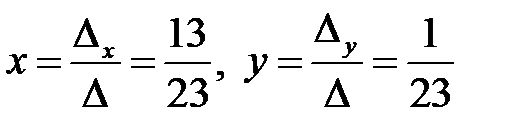 .
.
Ответ:  .
.
Система линейных неравенств с двумя неизвестными имеет вид:
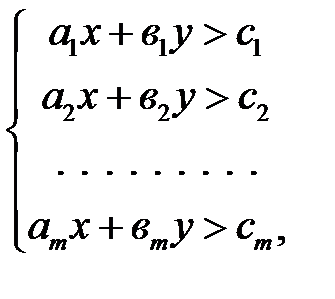 (2.2)
(2.2)
где  - коэффициенты системы;
- коэффициенты системы; 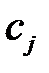 - свободные члены или правые части неравенств, - действительные числа. Так как решением каждого неравенства системы является полуплоскость, то решением системы служит многоугольник, координаты точек которого удовлетворяют каждому неравенству системы. Можно показать, что этот многоугольник выпуклый.
- свободные члены или правые части неравенств, - действительные числа. Так как решением каждого неравенства системы является полуплоскость, то решением системы служит многоугольник, координаты точек которого удовлетворяют каждому неравенству системы. Можно показать, что этот многоугольник выпуклый.
Пример 4. Решить систему неравенств. Многоугольник решений изобразить на чертеже.
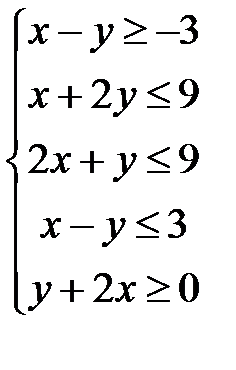
Решение. Найдем решение каждого неравенства системы. Заменим в каждом неравенстве знак неравенства на знак равно.
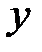
|
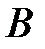
|

|

|
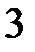
|

|

|

|

|

|

|
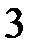
|

|
|
|

|
|

|
|
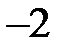
|
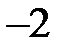
|
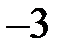
|
Рис. 3.
Решением служит многоугольник 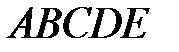 .
.
Дата добавления: 2015-04-15; просмотров: 253; Мы поможем в написании вашей работы!; Нарушение авторских прав |