Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений, содержащей 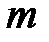уравнений с 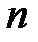неизвестными, называется система вида:

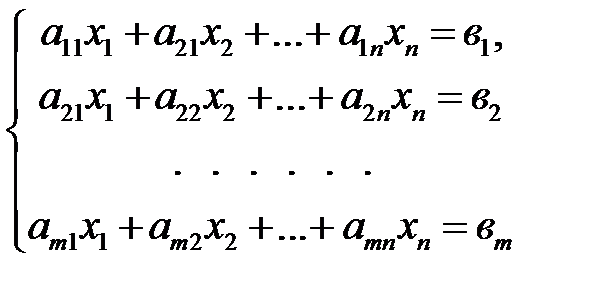(5.1).

Эту систему удобно записывать в виде одного матричного уравнения

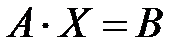(5.2).

Здесь 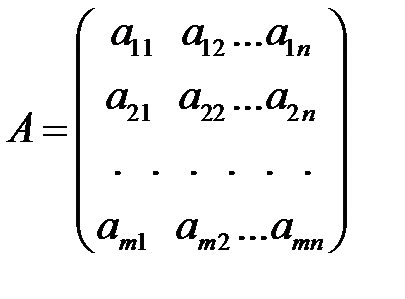- матрица системы,

- вектор-столбец неизвестных,

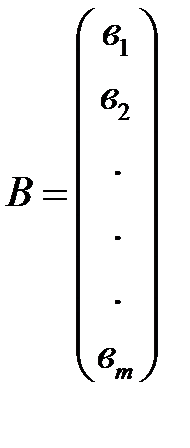- вектор-столбец свободных членов.

Величины 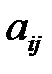, называемые коэффициентами системы, и величины , называемые свободными членами, предполагаются известными.

Система (5.1) называется однородной, если все ее свободные члены 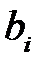равны нулю. Если хотя бы один из свободных членов отличен от нуля, то система называется неоднородной.

Система (5.1) называется квадратной, если число уравнений 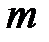равно числу неизвестных .

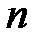Решением системы (5.1) называется такая совокупность 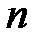чисел 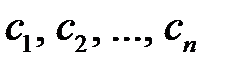, которая при подстановке в систему (5.1) на место неизвестных 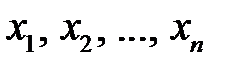обращает все уравнения системы в тождества.

Система (5.1) имеющая хотя бы одно решение, называется совместной системой. Система не имеющая решений называется несовместной.

Совместная система, имеющая единственное решение называется определенной. Система называется неопределенной, если она имеет более одного решения.

Рангом матрицы А называется наивысший порядок отличного от нуля минора.

Справедлива теорема Кронекера-Капелли .

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Здесь 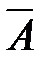- расширенная матрица.

Если ранг матрицы А равен рангу расширенной матрицы 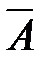и равен 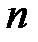- числу неизвестных, то система имеет единственное решение.

Если система совместна и ранг матрицы А меньше числа неизвестных 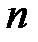, то система имеет множество решений.