Матрицы и определители

Матрицей порядка называют таблицу чисел, состоящую из 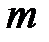- строк и - столбцов.

Числа, входящие в состав матрицы, называют элементами матрицы. Для обозначения матрицы используют заглавные буквы латинского алфавита . Элементы матрицы обозначают , где и называют индексом элемента . Первый индекс определяет номер строки, индекс - определяет номер столбца матрицы . Если число строк матрицы равно числу столбцов, то матрицу называют квадратной. Если матрица состоит из одной строки, ее называют матрица-строка, если матрица состоит из одного столбца, то ее называют матрицей-столбцом. Если у квадратной матрицы элементы при , то матрицу называют диагональной. Если у диагональной матрицы все элементы , то матрицу называют единичной матрицей. Единичную матрицу обозначают буквой . Например:

.

Матрицы одинакового порядка можно складывать и вычитать.

Суммой двух матриц и одинакового порядка называют матрицу того же порядка, элементы которой вычисляют по правилу

(3.1).

Аналогично определяют разность матриц.

Пример 5. Найти сумму и разность матриц и .

.

.

.

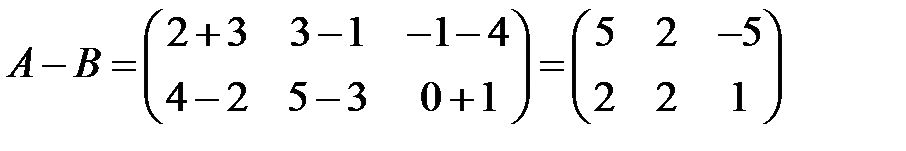Произведением матрицы на число называют матрицу , элементы которой вычисляют по формуле

(3.2).

Пример 6. Матрицу умножить на .

Решение. .

Произведением двух матриц порядка и порядка называют матрицу порядка , элементы которой определяют по формуле:

(3.3).

Замечание 1. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Пример 7. Найти произведение матриц и , если

.

Решение.

Квадратная матрица порядка называется обратной матрицей матрицы порядка , если .

Замечание 2. Произведение матриц не обладает свойством коммутативности, то есть в общем случае:

.

Если , то матрицы называют коммутативными.

Замечание 3. Для обратных матриц справедливо равенство .

Обратную матрицу принято обозначать .