
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Комплексные числа
Комплексным числом 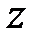 называется выражение
называется выражение
 (9.1),
(9.1),
где  и
и  - действительные числа;
- действительные числа; 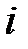 - мнимая единица, определяемая равенством
- мнимая единица, определяемая равенством
 или
или  (9.2).
(9.2).
Число  называют действительной частью комплексного числа
называют действительной частью комплексного числа 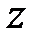 и обозначают
и обозначают  ;
;  - мнимая часть комплексного числа
- мнимая часть комплексного числа 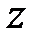 . Ее обозначают
. Ее обозначают 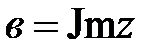 . Если
. Если 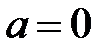 , то число
, то число  называют чисто мнимым, если
называют чисто мнимым, если 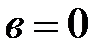 , то число
, то число 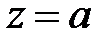 , есть действительное число.
, есть действительное число.
Два комплексных числа  и
и  называют комплексно сопряженными числами.
называют комплексно сопряженными числами.
Два комплексных числа  и
и 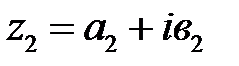 считаются равными, если
считаются равными, если  и
и  . Комплексное число
. Комплексное число 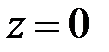 , если
, если 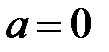 и
и 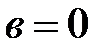 . Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Иногда комплексное число 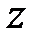 удобнее изображать в виде вектора
удобнее изображать в виде вектора 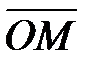 , начало которого совпадает с началом координат, соединяющего точку
, начало которого совпадает с началом координат, соединяющего точку  с точкой
с точкой  . Длина этого вектора называется модулем комплексного числа
. Длина этого вектора называется модулем комплексного числа 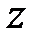 и обозначается
и обозначается 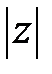 .
.
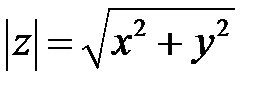 .
.
Угол  между осью
между осью  и вектором
и вектором 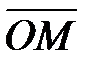 , отсчитанный против часовой стрелки, называется аргументом комплексного числа
, отсчитанный против часовой стрелки, называется аргументом комплексного числа 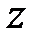 и обозначается
и обозначается 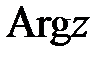 .
.
Аргумент числа 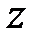 определяется с точностью до слагаемого
определяется с точностью до слагаемого 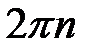 , где
, где  - целое число. Главное значение аргумента числа
- целое число. Главное значение аргумента числа 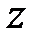 - значение аргумента, удовлетворяющее неравенству
- значение аргумента, удовлетворяющее неравенству 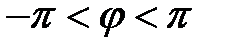 . Главное значение аргумента комплексного числа
. Главное значение аргумента комплексного числа 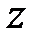 обозначается через
обозначается через 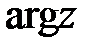 :
:  .
.
Запись числа 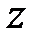 в виде
в виде 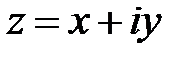 называют алгебраической формой записи комплексного числа.
называют алгебраической формой записи комплексного числа.
Сумма, разность комплексных чисел и умножение определяется так же, как действия над соответствующими векторами.
Суммой комплексных чисел 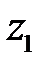 и
и  называется комплексное число
называется комплексное число
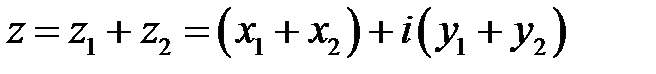 (9.3).
(9.3).
Разностью комплексных чисел 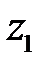 и
и  называется комплексное число
называется комплексное число
 (9.4).
(9.4).
Произведение комплексного числа 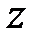 на действительное число
на действительное число 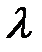 называется комплексное число
называется комплексное число  .
.
Произведение двух комплексных чисел 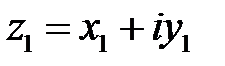 и
и  , записанных в алгебраической форме определяется как произведение двучленов:
, записанных в алгебраической форме определяется как произведение двучленов:
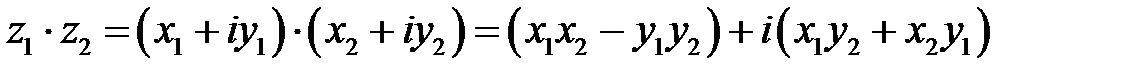 (9.5).
(9.5).
Произведением двух комплексно сопряженных чисел служит действительное число
 (9.6).
(9.6).
Деление комплексных чисел определяется, как действие обратное умножению. Частное двух комплексных чисел 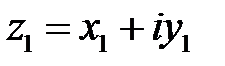 и
и  определяется следующим образом:
определяется следующим образом:
 (9.7).
(9.7).
Наряду с прямоугольной системой координат 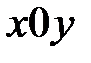 введем полярную систему, начало которой совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси
введем полярную систему, начало которой совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси  . Рис. 8.
. Рис. 8.

|
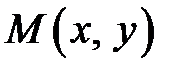
|
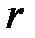
|

|

|

|
Рис. 8.
Из Рис.8 следует, что:
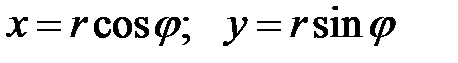 .
.
Подставляя 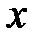 и
и  в алгебраическую форму комплексного числа, получим
в алгебраическую форму комплексного числа, получим
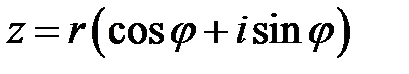 (9.8).
(9.8).
Выражение (9.8) называют тригонометрической формой записи комплексного числа 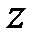 , где
, где 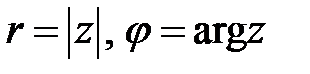 .
.
Пусть даны два комплексных числа  и
и  . Записанные в тригонометрической форме:
. Записанные в тригонометрической форме:
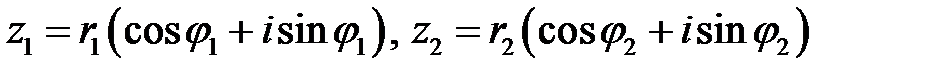 .
.
Тогда 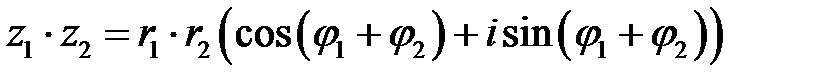 .
.
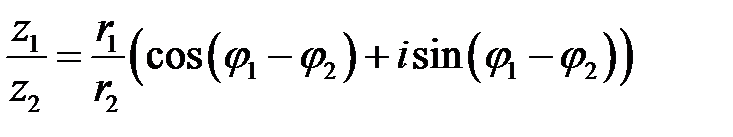 (9.9).
(9.9).
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Если  - целое положительное число, то из (9.9) следует:
- целое положительное число, то из (9.9) следует:
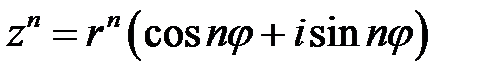 (9.10).
(9.10).
Корнем  -й степени из комплексного числа
-й степени из комплексного числа 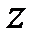 называется такое комплексное число
называется такое комплексное число 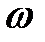 ,
,  -я степень которого равна
-я степень которого равна 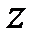 , т.е.
, т.е. 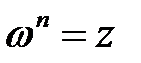 .
.
Корень  -й степени из
-й степени из 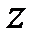 обозначается
обозначается 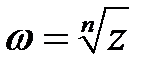 .
.
Если 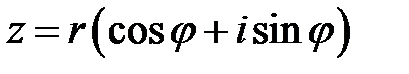 , то
, то  равен:
равен:
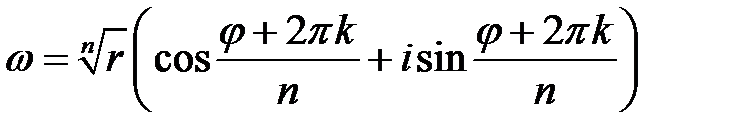 (9.11).
(9.11).
Подставляя в (9.11) значения 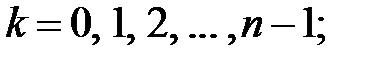 получим ровно
получим ровно  различных корней
различных корней  -й степени из
-й степени из 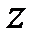 .
.
Пример 12. Дано комплексное число 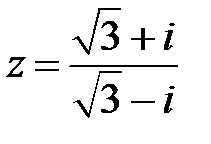 .
.
Записать число 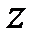 в алгебраической и тригонометрической формах. Найти все корни уравнения
в алгебраической и тригонометрической формах. Найти все корни уравнения  .
.
Решение. Запишем число 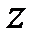 в алгебраической форме:
в алгебраической форме:
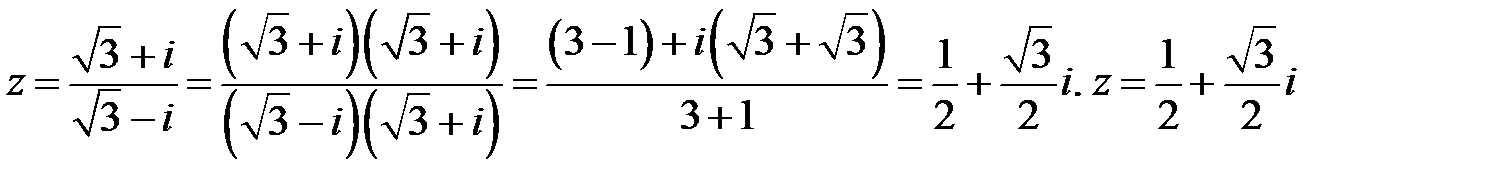 .
.
Найдем 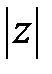 :
:  .
.
Вычислим  . Тригонометрическая форма записи комплексного числа
. Тригонометрическая форма записи комплексного числа 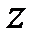 имеет вид:
имеет вид:
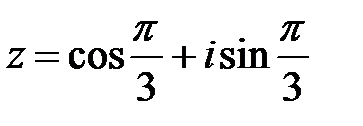 .
.
Вычислим  :
:

при 
при 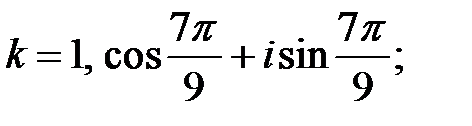
при 
Кроме алгебраической и тригонометрической форм записи комплексного числа 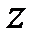 , применяется более короткая, так называемая показательная форма комплексного числа
, применяется более короткая, так называемая показательная форма комплексного числа 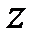 , согласно которой
, согласно которой
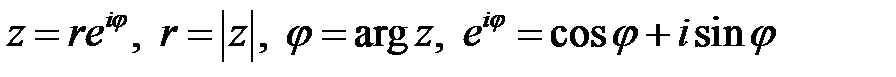 .
.
Пусть 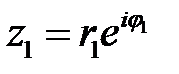 и
и 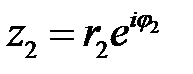 , тогда:
, тогда:
 .
.
Дата добавления: 2015-04-15; просмотров: 312; Мы поможем в написании вашей работы!; Нарушение авторских прав |