Различные уравнения прямой на плоскости.

1. Общее уравнение прямой на плоскости.

Всякое уравнение первой степени относительно х и у, то есть уравнение вида

, (11.1)

где – постоянные коэффициенты, причем 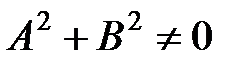, определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой. Справедливо и обратное утверждение: в декартовых координатах всякая прямая определяется уравнением первой степени относительно и .

2. Неполное уравнение прямой. Если в общем уравнении прямой (11.1) один или два из трех коэффициентов обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1) ; уравнение имеет вид и определяет прямую, проходящую через начало координат;

2) ; уравнение имеет вид и определяет прямую, параллельную оси ;

3) ; уравнение имеет вид 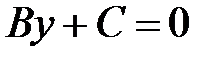и определяет прямую, параллельную оси ;

4) ; уравнение может быть записано в виде и определяет ось ;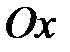

5) ; уравнение записывается в виде и определяет ось .

3. Уравнение прямой с угловым коэффициентом.

Если из общего уравнения прямой 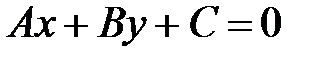выразить у как функцию переменной , то получим уравнение

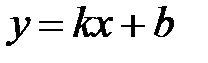, (11.2)

которое называют уравнением прямой с угловым коэффициентом. Угловой коэффициент равен тангенсу угла, образованного прямой с положительным направлением оси 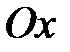. Коэффициент равен ординате точки пересечения прямой с осью .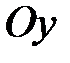

4. Уравнение прямой в отрезках.

Если в общем уравнении прямой 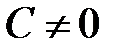, то поделив все члены уравнения на 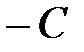, получим уравнение вида

(11.3)

которое называется уравнением прямой в отрезках, и - отрезки, отсекаемые прямой от осей координат .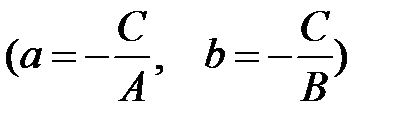

5. Нормальное уравнение прямой.

Если обе части общего уравнения прямой умножить на число , которое называют нормирующим множителем, то получим уравнение

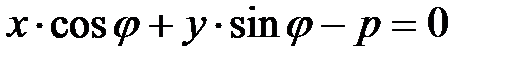. (11.4)

Это уравнение называют нормальным уравнением прямой. Знак нормирующего множителя выбирают из условия . Коэффициент в нормальном уравнении прямой равен длине перпендикуляра, опущенного из начала координат на прямую и определяет расстояние от начала координат до прямой; - угол, образованный этим перпендикуляром с положительным направлением оси .

6. Уравнение прямой, проходящей через две точки.

Если даны координаты двух точек М₁(х₁; у₁) и М₂(х₂; у₂), то уравнение прямой, проходящей через эти точки, записывается в виде:

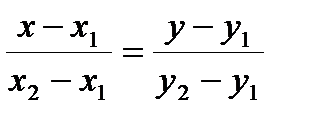. (11.5)

Если , то уравнение прямой, проходящей через точки и 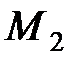имеет вид . Если , то уравнение имеет вид .

7. Каноническое уравнение прямой на плоскости.

Всякий ненулевой вектор , лежащий на данной прямой или параллельный данной прямой, называют направляющим вектором этой прямой. Уравнение прямой, проходящей через точку М₀(х₀; у₀) в направлении вектора 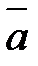имеет вид:

. (11.6)

Это уравнение называют каноническим уравнением прямой на плоскости.

8. Параметрические уравнения прямой на плоскости.

Если каждое из равных отношений в каноническом уравнении прямой обозначить буквой t и из полученных равенств выразить х и у, то получим систему:

(11.7)

Эту систему называют параметрическими уравнениями прямой на плоскости, проходящей через точку М₀(х₀; у₀) в направлении вектора .

9. Расстояние от точки 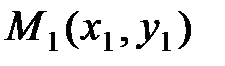до прямой Ах + Ву + С = 0 находится по формуле: .

Отклонением точки 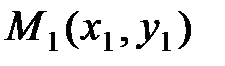от прямой Ах + Ву + С = 0 называют величину .

10. Угол между прямыми.

Две прямые на плоскости могут быть параллельными, совпадающими или пересекающимися. Если прямые заданы общими уравнениями

, , то:

1) если - прямые совпадают;

2) если - прямые параллельны;

3) если - прямые пересекаются.

Угол между прямыми можно определить по формуле:

.

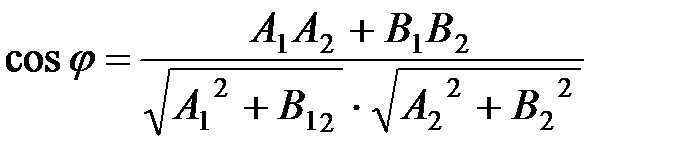Если , то прямые перпендикулярны.

Если прямые заданы уравнениями с угловыми коэффициентами

, то:

1) если - прямые параллельны;

2) если - прямые перпендикулярны;

3) если - прямые пересекаются.

Угол между прямыми определяется по формуле: .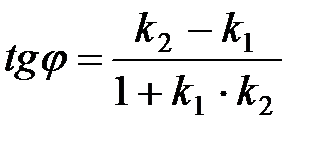

Если прямые пересекаются, то координаты точки пересечения определяют из системы: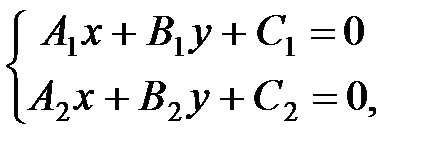

в случае задания прямых их общими уравнениями. Если прямые заданы уравнениями с угловыми коэффициентами, то система имеет вид:

Пример13. Даны вершины треугольника А(-5; 10), В(5; 16), С(3; 2). Написать:

1) уравнения сторон треугольника;

2) уравнения медианы и высоты, проведенных из вершины А;

3) уравнение биссектрисы угла С;

4) вычислить длину высоты и медианы, проведенных из вершины А.

Решение.

1). Запишем уравнение стороны АВ: так как координаты вершин А и В известны, то воспользуемся уравнением прямой , проходящей через две точки:

или преобразуя получим

Запишем уравнение стороны АС: или

Запишем уравнение стороны ВС: , или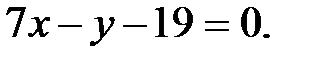

2). Вычислим координаты М середины стороны ВС:

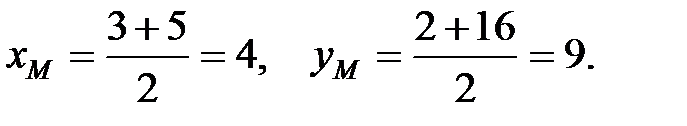
Длину медианы АМ вычислим по формуле:

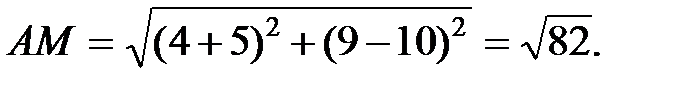
Запишем уравнение медианы АМ: 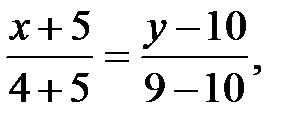или

Вычислим угловой коэффициент прямой ВС. Для этого выразим у из ее уравнения: ,

тогда угловой коэффициент . Высота, опущенная из вершины угла А, перпендикулярна стороне ВС. Ее угловой коэффициент найдем из условия перпендикулярности: . Тогда .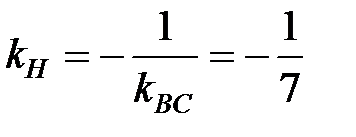

Запишем уравнение высоты, как уравнение прямой , проходящей через точку А(-5; 10) с угловым коэффициентом : .

Определим из условия, что точка А принадлежит прямой

Подставляя в уравнение высоты, получим: или .

3). По свойству биссектрисы внутреннего угла треугольника, имеем:

, где D – точка пересечения биссектрисы со стороной АВ.

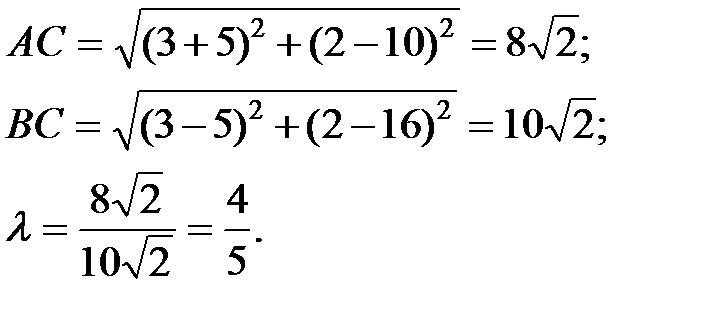
Найдем координаты точки D по формулам деления отрезка в данном отношении:

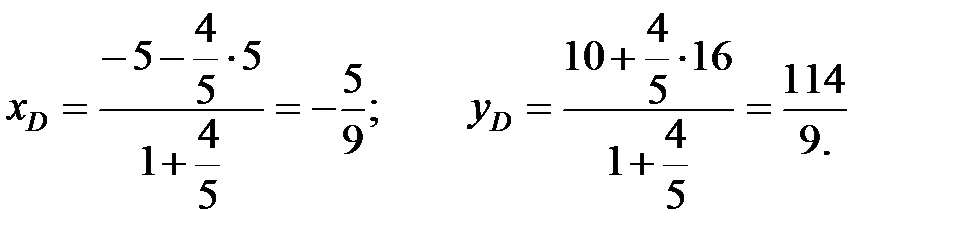
Запишем уравнение биссектрисы СD:

, или после преобразования,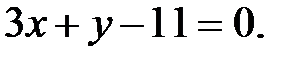

4). Длина высоты равна расстоянию d точки А от прямой ВС. Запишем нормальное уравнение прямой ВС:

Длина медианы АМ найдена в пункте 2.

Ответ: 1) , , ;

2) - уравнение медианы,

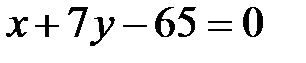- уравнение высоты;

3) - уравнение биссектрисы угла С;

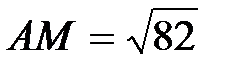4) - длина высоты; - длина медианы.