
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поверхности второго порядка.
Поверхностью второго порядка называют совокупность точек пространства, координаты которых x, y, z удовлетворяют уравнению

Коэффициенты  могут принимать любые действительные значения и удовлетворяют условию
могут принимать любые действительные значения и удовлетворяют условию  .
.
Для определения вида поверхности второго порядка необходимо ее уравнение привести к виду, не содержащему произведений координат. Этого можно достичь соответствующим выбором системы координат.
 называют квадратичной формой. Матрицу
называют квадратичной формой. Матрицу
 ,
,
где  , называют матрицей квадратичной формы. Вектор
, называют матрицей квадратичной формы. Вектор  , удовлетворяющий условию
, удовлетворяющий условию  называют собственным вектором матрицы А,
называют собственным вектором матрицы А, 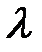 - собственным значением.
- собственным значением.
Каждая матрица квадратичной формы имеет три взаимно ортогональных собственных вектора. Если единичные векторы собственных векторов матрицы А принять за единичные векторы новой системы координат, то в выражении квадратичной формы коэффициенты при произведениях обратятся в ноль и форма примет вид:
 .
.
Присоединяя к ней линейную часть общего уравнения поверхности второго порядка и выделяя полные квадраты, получим каноническое уравнение поверхности второго порядка.
Пример 24. Привести к каноническому виду уравнение поверхности:
3x2 +5y2 +3z2 – 2xy + 2xz – 2yz -12x – 10 = 0.
Решение.
Составим матрицу А:
 .
.
Найдем собственные векторы:


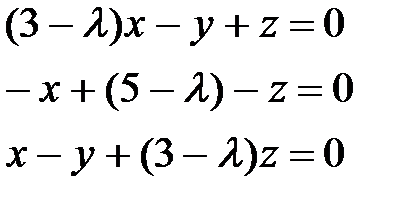
Полученная система имеет ненулевые решения, если ее определитель равен нулю, т.е.

Раскрывая определитель, получим:
 .
.
Отсюда находим:  .
.
При  получим систему уравнений:
получим систему уравнений:

Решив систему, получим первый собственный вектор  . Единичный вектор
. Единичный вектор  собственного вектора
собственного вектора  будет:
будет:  .
.
При  получим
получим 
При  получим
получим  .
.
Записывая координаты единичных векторов в соответствующие столбцы, получим матрицу преобразования S:

Отсюда получим формулы преобразования координат:



Подставим значения  ,
, 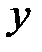 и
и  в уравнение поверхности:
в уравнение поверхности:

или 
Перепишем уравнение в виде:

Дополнив выражение в каждой скобке до полного квадрата, получим:

Совершив параллельный перенос осей координат и разделив на 24 обе части уравнения, получим

Это уравнение описывает поверхность, называемую эллипсоидом.
Классификация поверхностей второго порядка.
Применяя преобразование координат, уравнение поверхности второго порядка всегда можно привести к виду:
 .
.
В зависимости от величины и знаков коэффициентов  ,
,  ,
,  ,
,  ,
,  ,
,  и
и  могут представиться следующие частные случаи уравнений поверхностей второго порядка.
могут представиться следующие частные случаи уравнений поверхностей второго порядка.
Таблица 1.
1. Эллипсоиды:

 трехосный эллипсоид,
трехосный эллипсоид,
 мнимый эллипсоид
мнимый эллипсоид
 точка
точка 
 2. Гиперболоиды:
2. Гиперболоиды:
1)  однополостные гиперболоиды
однополостные гиперболоиды

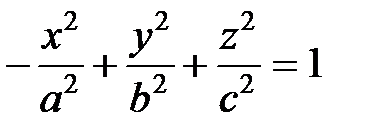
 2)
2)  двуполостные гиперболоиды
двуполостные гиперболоиды


3. Конусы:




4. Параболоиды:
 1)
1)  эллиптические параболоиды
эллиптические параболоиды


 2)
2)  гиперболические параболоиды
гиперболические параболоиды
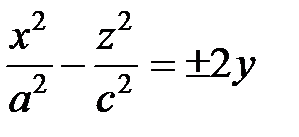


5. Цилиндры
1)  эллиптические цилиндры
эллиптические цилиндры


 2)
2)  гиперболические цилиндры
гиперболические цилиндры
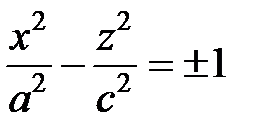

 3)
3)  - параболические цилиндры
- параболические цилиндры
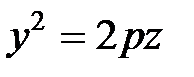




 6. Пары плоскостей:
6. Пары плоскостей:
1)  - пары пересекающихся плоскостей
- пары пересекающихся плоскостей

 2)
2)  - пары параллельных плоскостей
- пары параллельных плоскостей

 3)
3)  - пары совпадающих плоскостей
- пары совпадающих плоскостей

Дата добавления: 2015-04-15; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |