Прямая в пространстве. Две плоскости, если они не параллельны и не совпадают, пересекаются по прямой

Две плоскости, если они не параллельны и не совпадают, пересекаются по прямой. Эту прямую можно описать системой вида:

, (14.1)

где - уравнение одной из пересекающихся плоскостей, - уравнение другой плоскости. Систему двух уравнений с тремя неизвестными называют общим уравнением прямой в пространстве. Известно, что система двух линейных уравнений с тремя неизвестными имеет множество решений, если она совместна. Из всего множества решений всегда можно выделить два различных, что геометрически будет соответствовать двум различным точкам М₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), принадлежащим данной прямой. Через две точки проходит единственная прямая, уравнение которой имеет вид:

. (14.2)

Определим вектор , параллельный данной прямой, который будем называть направляющим вектором. Из условия параллельности получим:

, (14.3)

где М(x₀,y₀,z₀) – точка, расположенная на прямой.

Полученные уравнения называют каноническими уравнениями прямой в пространстве. Обозначая коэффициент пропорциональности в канонических уравнениях прямой через t, получим:

. (14.4)

Полученную систему называют параметрическими уравнениями прямой в пространстве. Углом между двумя прямыми называют угол между их направляющими векторами. Если прямые заданы каноническими уравнениями и ,

то угол φ между ними определяется по формуле:

.

Если , то прямые перпендикулярны.

Если , то прямые параллельны.

Необходимым и достаточным условием принадлежности двух прямых, заданных каноническими уравнениями, одной плоскости, служит равенство:

.

Если прямая 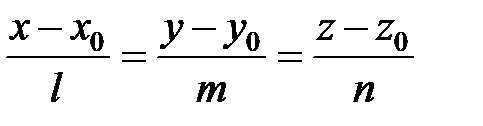пересекает плоскость Ax + By + Cz + D = 0, то угол , образованный прямой и плоскостью, определяют из равенства: .

- условие параллельности прямой и плоскости;

- условие перпендикулярности прямой и плоскости.

Если , то прямая пересекает плоскость Ax + By + Cz + D = 0. Точку пересечения прямой и плоскости можно определить из системы:

Условия принадлежности прямой плоскости Ax + By + Cz + D = 0 имеют вид:

Расстояние d от точки М₁(x₁, y₁, z₁) до прямой, заданной каноническими уравнениями 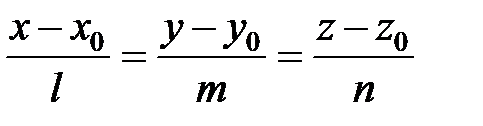, находится по формуле:

.

Расстояние h между двумя скрещивающимися прямыми, заданными каноническими уравнениями, определяют по формуле:

, где - точка, принадлежащая первой прямой, - точка, принадлежащая второй прямой.

Пример 22. Даны вершины треугольника А(1; -2; -4), В(3; 1; -3) и С(5; 1; -7). Составить параметрические уравнения высоты, опущенной из вершины В на противоположную сторону.

Решение.

Составим уравнение плоскости, проходящей через точку В, перпендикулярно стороне АС, Нормальный вектор этой плоскости . Уравнение плоскости , или .

Запишем уравнение прямой АС:

, или в параметрическом виде:

Найдем точку пересечения М прямой АС и плоскости, перпендикулярной этой прямой, то есть основание высоты:

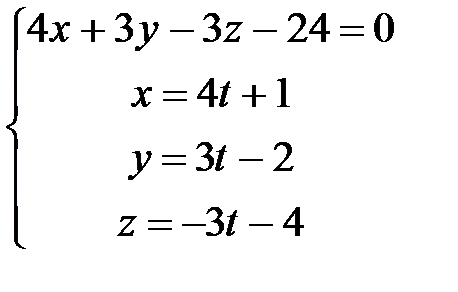
Подставим x, y, z в первое уравнение:

Найдем направляющий вектор высоты ВМ:

.

Возьмем вектор, коллинеарный вектору :

Параметрические уравнения высоты ВМ имеют вид:

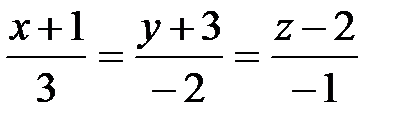Пример 23. Составить уравнения прямой, которая проходит через точку и пересекает прямые и .

Решение. Запишем уравнение плоскости, проходящей через прямую и точку М(-4; -5; 3). Точка М₁(-1; -3; 2) - принадлежит прямой и плоскости. Вектор =(3; 2; -1) так же принадлежит этой плоскости. За нормальный вектор плоскости возьмем вектор , равный векторному произведению вектора 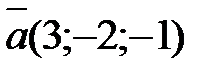и вектора :

.

Уравнение плоскости с нормальным вектором , проходящей через точку М(-4; -5; 3) имеет вид: 4(х + 4)+12(z – 3)= 0, или х + 3z – 5 = 0.

Найдем точку К пересечения плоскости х + 3z – 5 = 0 и прямой

:

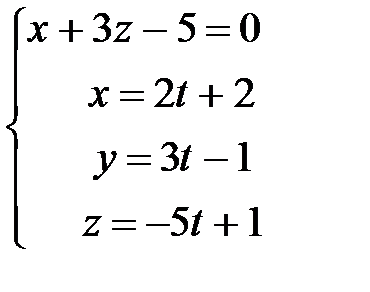Решим систему:

откуда . Прямая, проходящая через точки М(-4; -5; 3) и К(2; -1; 1) будет искомой. Уравнения этой прямой имеют вид:

или .