Полярная система координат.

Определение положения точки М с помощью декартовых координат не является единственным способом. Пусть дана некоторая плоскость. Выберем на ней точку О, из нее проведем луч ОЕ. На этом луче выберем единицу масштаба. Тогда любая точка М плоскости будет однозначно определена, если известно ее расстояние от точки О, то есть длина отрезка ОМ, и угол φ, образованный лучом ОЕ и отрезком ОМ. Пара чисел и называется полярными координатами точки М: φ – полярный угол, ρ – полярный радиус, луч ОЕ – полярная ось, точка О – полюс. Угол φ считается положительным, если он отсчитывается от полярной оси в направлении, противоположном направлению часовой стрелки. Область изменения полярных координат определяется системой неравенств: .

Если полюс полярной системы координат совместить с началом некоторой декартовой системы, заданной на той же плоскости, а полярную ось направить по оси ОХ, то полярные координаты 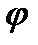и некоторой точки М будут связаны с декартовыми координатами х и у следующими соотношениями:

Если известны полярные координаты 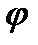и , то декартовы координаты х и у точки М вычисляются по формулам:

Пример 25. Найти полярные координаты точки М(1; - ), если полюс совпадает с началом координат, а полярная ось - с положительным направлением оси абсцисс.

Решение.

Имеем

угол находится в четвертой четверти, то есть

Ответ: М( ).