
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 4 (2 класс).
Направлено на выявление способности совмещения двух аспектов, а также выявляет комбинаторные способности детей.
Задание: Какие числа меньше 100, можно записать с помощью цифр 1, 2, 3? (Использовать можно только указанные цифры).
Пояснение к заданию: задание имеет 12 решений – однозначные числа 1, 2, 3 и двузначные – 11, 12, 13, 21, 22, 23, 31, 32, 33. все остальные решения являются неправильными, т. к. не соответствует ни одному из условий задачи (например, в числе 42 использована лишняя цифра 4, в числе 231 использованы нужные цифры, но число больше 100).
Уровни выполнения задания.
0 уровень – не найдено ни одно правильного решения, что свидетельствует о неспособности ученика воспринимать задание, требующей одновременной ориентации на два условия.
1 уровень – найдено 1-3 решения, ученик воспринимает оба условия задания, но комбинаторные способности находятся на очень низком уровне.
2 уровень – найдено 4-410 решений, ученик свободно владеет материалом задания, комбинаторные способности выражены достаточно ярко, но владение приемами исчерпывания решений недостаточно сформировано.
3 уровень – найдено 11-12 решений, характеризуется хорошее развитие комбинаторных способностей применительно к заданию, требующему ориентации на два признака.
В конце 1 полугодия 2 класса был проведён контрольный эксперимент. С учащимися экспериментального класса, обучающегося по математике по учебникам Аргинской И. И., и контрольного класса, обучающегося по традиционной системе, было проведено тестирование на определение уровня развития всех трёх видов мышления: наглядно-действенного, наглядно-образного и словесно-логического.
Тест: «Вырежи фигуры».
Время проведения: 16-17 января 2008 год.
Цель: оценка наглядно-действенного мышления
Инструкция: предложить ребенку как можно быстрее и точнее вырезать из бумаги нарисованные на ней фигуры. Все линии необходимо стараться делать прямыми. Оцениваться в итоге выполнения задания будут аккуратность, точность и скорость работы. Оценки даются в баллах в зависимости от скорости и качества (точности) выполнения задания.
Оценка результатов теста.
10 баллов - ребенок затратил на выполнение всего задания меньше,чем 90 сек, причем все линии на рисунке прямые и точно соединяют углы фигур. Все линии следуют точно по заданным контурам
8-9 баллов - на выполнение задания ушло от 90 до 105 сек. При этом имеет место хотя бы один из следующих недостатков: одна или две линии не являются вполне прямыми; в двух или в трех случаях начертанные линии не вполне правильно соединяют углы фигур; от двух до четырех линий выходят за пределы контура; от четырех до пяти углов соединены неточно.
6-7 баллов - на выполнение всего задания в целом ушло от 105 до 120 сек.При этом дополнительно обнаружен хотя бы один из следующих недочетов: три или четыре линии непрямые; от четырех до шести углов соединены не вполне точно; от пяти до шести линий выходят за пределы контура; от шести до семи углов соединены
не вполне точно.
4-5 баллов - на выполнение задания затрачено от 120 до 135 сек. Имеется хотя бы один из следующих недочетов: пять или шесть линий не являются вполне прямыми; от семи до десяти углов соединены не вполне правильно ;есть семь или восемь линий, которые не являются вполне прямыми; имеется от восьми до десяти углов,
которые соединены не вполне точно.
2-3 балла - на выполнение задания ушло от 135 до 150 сек. Отмечен хотя бы один из следующих недостатков: от семи до десяти линий непрямые; от одиннадцати до двадцати углов соединены не вполне правильно; от девяти до восемнадцати линий выходят за пределы контура; от одиннадцати до семнадцати углов соединены не вполне правильно.
0-1 балл - на выполнение задания ушло более 150 сек. Почти все линии, за исключением одной или двух, не являются прямыми; почти все углы, за исключением одного или двух, соединены неправильно.
Выводы об уровне развития наглядно-действенного мышления:
10 баллов - очень высокий.
8-9 баллов - высокий.
4-7 баллов - средний.
2-3 балла - низкий.
0-1 балл - очень низкий.
Полученные результаты:
| Экспериментальный класс (учебники Аргинской И. И.) | Контрольный класс (традиционная система) | ||||
| № | имя уч-ся | кол-во баллов | № | имя уч-ся | кол-во баллов |
| Никита А. | Алёша Б. | ||||
| Юля А. | Таня Б. | ||||
| Слава Б. | Таня Б. | ||||
| Ира Б. | Анна В. | ||||
| Олег Д. | Слава Г. | ||||
| Юля К. | Регина Г. | ||||
| Илья К. | Наташа Г. | ||||
| Жанна К. | Ольга Д. | ||||
| Максим К. | Вова Е. | ||||
| Полина К. | Ольга К. | ||||
| Ольга М. | Саша К. | ||||
| Илья Н. | Иван К. | ||||
| Дарья Н. | Яна К. | ||||
| Ульяна Н. | Маша Л. | ||||
| Анна У. | Ринат М. | ||||
| Саша Х. | Ольга Н. | ||||
| Пётр Ч. | Саша П. | ||||
| Сергей Ш. | Алёна П. | ||||
| Ангелина Я. | Лена П. | ||||
| Вероника Я. | Яна С. | ||||
| Таня Т. | |||||
| Миша Р. | |||||
| Рустам У. | |||||
| Дима Ф. | |||||
| Никита Ч. | |||||
| Кол-во тестируемых – 20 (100%) Высокий, очень высокий – 18 (90%) Средний – 2 (10%) | Кол-во тестируемых – 25 (100%) Высокий, очень высокий – 17 (68%) Средний – 8 (32%) |
При проведении эксперимента установили: в экспериментальном классе, в котором математика изучается по учебникам Аргинской И. И., на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития наглядно-действенного мышления у 18 учащихся, что составляет 90%; в контрольном классе, в котором обучение ведётся по традиционной системе, на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития наглядно-действенного мышления у 17 учащихся, что составляет 68%.
Тест: «Что здесь лишнее?»
Время проведения: 23-24 января 2008 года.
Цель: оценка наглядно-образного мышления.
Инструкция: детям предлагается серия картинок, на которых представлены разные предметы, причем один из них лишний. Например:
изображение белого гриба, подберезовика, цветка и мухомора;
кастрюля, чашка, ложка, шкаф; стол, стул, кровать, кукла. Ребёнок должен назвать лишний предмет. Возможная помощь в дополнительных вопросах отсутствует.
Оценка результатов теста: за каждый правильный ответ - 1 балл; за каждый неправильный ответ - 0 баллов.
Выводы об уровне развития наглядно-образного мышления:
10 баллов - очень высокий.
8-9 баллов - высокий.
4-7 баллов - средний.
2-3 балла - низкий.
0-1 балл - очень низкий.
| Экспериментальный класс (учебники Аргинской И. И.) | Контрольный класс (традиционная система) | ||||
| № | имя уч-ся | кол-во баллов | № | имя уч-ся | кол-во баллов |
| Никита А. | Алёша Б. | ||||
| Юля А. | Таня Б. | ||||
| Слава Б. | Таня Б. | ||||
| Ира Б. | Анна В. | ||||
| Олег Д. | Слава Г. | ||||
| Юля К. | Регина Г. | ||||
| Илья К. | Наташа Г. | ||||
| Жанна К. | Ольга Д. | ||||
| Максим К. | Вова Е. | ||||
| Полина К. | Ольга К. | ||||
| Ольга М. | Саша К. | ||||
| Илья Н. | Иван К. | ||||
| Дарья Н. | Яна К. | ||||
| Ульяна Н. | Маша Л. | ||||
| Анна У. | Ринат М. | ||||
| Саша Х. | Ольга Н. | ||||
| Пётр Ч. | Саша П. | ||||
| Сергей Ш. | Алёна П. | ||||
| Ангелина Я. | Лена П. | ||||
| Вероника Я. | Яна С. | ||||
| Таня Т. | |||||
| Миша Р. | |||||
| Рустам У. | |||||
| Дима Ф. | |||||
| Никита Ч. | |||||
| Кол-во тестируемых – 20 (100%) Высокий, очень высокий – 13 (65%) Средний – 17 (35%) | Кол-во тестируемых – 25 (100%) Высокий, очень высокий – 10 (40%) Средний – 15 (60%) |
При проведении эксперимента установили: в экспериментальном классе, в котором математика изучается по учебникам Аргинской И. И., на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития наглядно-образного мышления у 13 учащихся, что составляет 65%; в контрольном классе, в котором обучение ведётся по традиционной системе, на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития наглядно-образного мышления у 10 учащихся, что составляет 40%.
Тест: «Ответь на вопросы»
Время проведения: 30-31 января 2008 года.
Цель: оценка словесно-логического мышления.
Инструкция: Ребенку предлагается ответить на следующие вопросы. Если ребёнок затрудняется, то попробуйте вместе поискать ответы. О высоком уровне словесно-логического мышления у ребенка можно говорить, если он дает правильные ответы на 95% вопросов.
Что из чего делают?
(В скобках даны возможные правильные ответы. )
· Что делают из муки? (хлеб,...)
· Что делают из молока? (творог,...)
· Что делают из шерсти овец и коз? (шерстяные нитки,...)
· Что делают из шерстяных ниток? (носки,...)
· Что делают из песка? (стекло,...)
· Что делают из глины? (кирпич,...)
· Что делают из металла? (инструменты,...)
· Что делают из нефти? (бензин,...)
· Что делают из хлопка? (ткань,...)
· Что делают из древесины? (мебель,...)
· Что делают из семян подсолнуха? (подсолнечное масло,...)
Что с чем делают?
· Песок сыплют, а воду ...
· Стол накрывают, а постель ...
· Котлеты жарят, а суп ...
· Цветы водой поливают, а огонь ...
· Нитку в иголку вдевают, а гвоздь в стену ...
· Воду можно разлить, а горох ...
· Стол можно сломать, а стакан ...
· Сено косят, а волосы ...
· Нитки прядут, а холст ...
· Платье шьют, а шарф ...
Выводы об уровне развития словесно-логического мышления:
4-5 баллов - очень высокий.
3 балла - высокий.
1-2 балла - средний.
0 баллов - низкий.
| Экспериментальный класс (учебники Аргинской И. И.) | Контрольный класс (традиционная система) | ||||
| № | имя уч-ся | кол-во баллов | № | имя уч-ся | кол-во баллов |
| Никита А. | Алёша Б. | ||||
| Юля А. | Таня Б. | ||||
| Слава Б. | Таня Б. | ||||
| Ира Б. | Анна В. | ||||
| Олег Д. | Слава Г. | ||||
| Юля К. | Регина Г. | ||||
| Илья К. | Наташа Г. | ||||
| Жанна К. | Ольга Д. | ||||
| Максим К. | Вова Е. | ||||
| Полина К. | Ольга К. | ||||
| Ольга М. | Саша К. | ||||
| Илья Н. | Иван К. | ||||
| Дарья Н. | Яна К. | ||||
| Ульяна Н. | Маша Л. | ||||
| Анна У. | Ринат М. | ||||
| Саша Х. | Ольга Н. | ||||
| Пётр Ч. | Саша П. | ||||
| Сергей Ш. | Алёна П. | ||||
| Ангелина Я. | Лена П. | ||||
| Вероника Я. | Яна С. | ||||
| Таня Т. | |||||
| Миша Р. | |||||
| Рустам У. | |||||
| Дима Ф. | |||||
| Никита Ч. | |||||
| Кол-во тестируемых – 20 (100%) Высокий, очень высокий – 5 (25%) Средний – 15 (75%) | Кол-во тестируемых – 25 (100%) Высокий, очень высокий – 3 (12%) Средний – 18 (72%) Низкий – 4 (16%) |
При проведении эксперимента установили: в экспериментальном классе, в котором математика изучается по учебникам Аргинской И. И., на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития словесно - логического мышления у 5 учащихся, что составляет 25%; в контрольном классе, в котором обучение ведётся по традиционной системе, на конец 1 полугодия 2 класса зафиксированы результаты высокого и очень высокого уровня развития словесно-логического мышления у 3 учеников, что составляет 12%.
На основе результатов используемых диагностик, получена следующая таблица результатов:
| Наглядно-действенное | Наглядно-образное | Словесно-логическое | |
| начало 1 класса | С 50% - до 75% С 40% - до 48% | 40% 24% | 10% 4% |
| конец 1 полугодия 2класса | 90% 68% | 65% 40% | 25% 12% |
Выше – данные экспериментального класса,ниже – контрольного класса.
Проанализируем данные результаты.
Наглядно-действенное мышление.
Сопоставляя динамику развития наглядно-действенного мышления у детей при обучении по разным программам, можно выделить некоторые различия. Так, при использовании в обучении математики учебников Аргинской И. И. наибольший рост детей, обладающих наглядно-действенным мышлением за один учебный год приходится на 1-ый класс (25%), при обучении по обычной программе – на 2-ой класс (20%). Можно утверждать, что с опозданием на один год при обучении по обычной программе воспроизводится приблизительно такое же число детей с наглядно-действенным мышлением, как при обучении математики по учебникам Аргинской И. И.. Это показывает, что обучение младших школьников математике по учебникам Аргинской И. И. способствует более интенсивному развитию у учащихся наглядно-действенного мышления.
Наглядно-образное мышление.
Рассмотрим данные, характеризующие развитие этого вида мышления у младших школьников. Прирост детей, обладающих наглядно-образным мышлением в экспериментальном классе - 25%, а в контрольном классе – 16%. Обращает внимание на себя тот факт, что число детей, обладающих наглядно-образным мышлением в экспериментальном классе после первого и второго годов обучения приблизительно равно числу учащихся, обладающих наглядно-действенным мышлением в контрольном классе. Это свидетельствует о том, обучение школьников математике по учебникам Аргинской И. И. создаёт большие возможности для развития наглядно-образного мышления, чем обучение по обычной программе.
Словесно-логическое мышление.
Рассмотрим данные по развитию у детей данного вида мышления. Обращает внимание тот факт, что за время обучения во 2-ом классе прирост учащихся, обладающих словесно-логическим мышлением, в экспериментальном классе больше, чем в контрольном классе (15%и 8%).
Отмеченные факты свидетельствуют о том, что обучение младших школьников математике по учебникам Аргинской И. И. в большей степени способствует переходу детей от наглядно-действенного к словесно-логическому мышлению, чем обучение по традиционной программе. Т. к. используется специально подобранная система заданий, способствующая переходу от наглядно-действенного к словесно-логическому мышлению младших школьников при решении задач сначала в ситуации, когда ученику есть возможность оперировать реальными предметами (т.е. решать задачу в наглядно-действенной форме), затем оперировать наглядными образами (т.е. решать задачу в наглядно-образной форме) и затем уж выполнять операции в форме абстрактных понятий и рассуждений (т.е. – в словесно-логической форме).
Заключение.
В конце 1 полугодия 2 класса была проведена диагностика в экспериментальном классе (обучение математике по учебникам Аргинской И. И.) и контрольном классе (традиционное обучение).
Цель: выяснить, насколько процесс мыслительной деятельности перешёл во внутренний план. Ведь возможно, что ошибки при обучении возникают у ребёнка именно при переходе мыслительной деятельности из внешнего плана (при образном мышлении) во внутренний (при словесном мышлении). Когда ему надо опираться только на словесно - оформленные логические операции, без опоры на внешний образ предмета.
Для эксперимента была использована
методика «Внутренний план действий», предложенная Л.М.Фридманом.
Цель: установить уровень развития у учащихся экспериментального класса (обучение математике по учебникам Аргинской И. И.) и контрольного класса (традиционное обучение) умения производить последовательность действий «в уме».
Ход эксперимента: ученикам предлагают решить, не глядя на доску ряд постоянно усложняющихся выражений на действия с натуральными числами в пределах 1-ой сотни за определённое время.
Выражения, н-р, такие:
1) 48+37
2) 50+15-9
3) 56-40+27
4) 86-(30-10)
5) (2+7)+ (20-19) и т. д.
Если ученик, не глядя на доску, решить выражение не может, то ему предлагают решить пример в уме, посмотрев его на доске.
Обработка полученных данных: уровень развития внутреннего плана действий определяется по номеру того примера из ряда усложняющихся, который ученик мог решить правильно, но следующий решить уже не сумел.
Результаты проведённого эксперимента представлены в виде графиков. По вертикали отмечены порядковые номера примеров, по горизонтали – количество учащихся, дошедших до какого-либо примера.

При проведении этой опытно-экспериментальной работы зафиксировано:
- общее количество устно решённых выражений всеми
учащимися экспериментального класса……………………171 (85% от всех)
- общее количество устно решённых выражений всеми
учащимися контрольного класса……………………………100 (50% от всех)
- количество детей в экспериментальном классе,
решивших максимальное количество выражений………….3 (15%)
- количество детей в контрольном классе,
решивших максимальное количество задач…………………0 (0%)
Ученики контрольного класса (традиционное обучение), испытывали больше трудностей в выполнении мыслительных операций и не достигли уровня решения примеров учениками экспериментального класса(обучение математике по учебникам Аргинской И. И).Это всё говорит не о единичных успехах, а об общем более высоком уровне развития у детей экспериментального класса умения производить последовательность действий «в уме».
Для подтверждения верности высказанной гипотезы исследовательской работы, была проведена диагностика в экспериментальном классе (обучение математике по учебникам Аргинской И. И.) и контрольном классе (традиционное обучение) по
методике В.В.Давыдова «Параллельное перемещение коня».
Цель: выяснить особенности перехода младших школьников от наглядно-образного мышления к словесно-логическому
Ход эксперимента: ученикам предлагаются 8 задач, для решения которых требуется в умственном плане оперировать представляемым предметом (он носит название «шахматный конь», т.к. перемещение делается по правилам хода этой фигуры).
Эксперимент проходил фронтально. К нему привлекались из экспериментального и контрольного классов по 10 учащихся, знания которых оцениваются отметками «4» и «5». Вначале экспериментатор рисовал игровое поле.
| А | Б | В | Г |
Затем разъяснял детям названия клеток (сочетание буквы и цифры), показывал ход шахматного коня, объяснял, как перемещается конь в два хода, и как эти ходы записываются. Дети получили бланки с заданиями:
Тренировочные задачи.
1. Указать клетки, куда конь может попасть за один ход из клетки Б-7.
2. Указать клетки, куда конь может попасть за один ход из клетки В-1.
Основные задачи.
1. А-7 --------? --------В-7.
2. А-6 --------? --------В-6.
3. А-5---------? --------В-5.
4. А-7 --------? --------? --------Г-5.
5. А-6 --------? --------? --------Г-4.
6. А-5 --------? --------? --------Г-3.
Тренировочные задачи проверялись у каждого ученика, ошибки исправлялись. Основные задачи дети решали самостоятельно после объяснения, что задачи 1-3 решаются в два действия, а задачи 4-6 – в три действия.
Обработка полученных данных: если ребёнок успел решить все 6 основных задач верно, то считается, что испытуемый действовал теоретическим способом, выявляя общий принцип решения. Если ребёнок решил не все задачи или некоторые задачи решил неверно, то полагается, что в этом случае школьник действовал эмпирическим способом, когда каждая задача решается в отдельности и как самостоятельная.
Результаты эксперимента представлены в графике процентными данными.
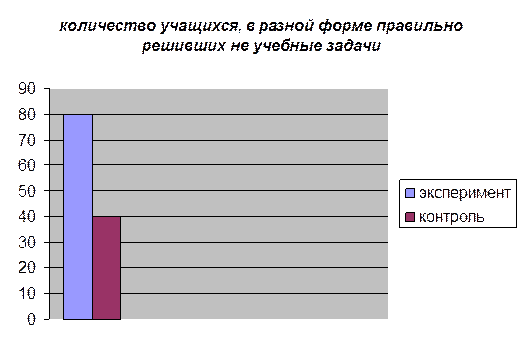
Полученные результаты опытно-экспериментальной работы свидетельствуют о том, что обучение младших школьников математике по учебникам Аргинской И. И. создает большие возможности для осуществления теоретического способа решения задач, чем обучение по обычной программе.
Экспериментальными исследованиями показана правильность выдвинутой гипотезы о том, что если целенаправленно и систематически использовать задания, решение которых направлено на формирование таких мыслительных операций, как рассмотрение ряда предметов под одним и тем же углом зрения, классификация их по общности в одном признаке, переключение с одного аспекта рассмотрения на другой, осмысление конкретной ситуации с точки зрения математической зависимости, которые выступают в многообразных соотношениях наглядно-действенного, наглядно-образного и словесно-логического мышления, то процесс развития различных видов мышления будет иметь качественные изменения от низшего (наглядно-действенного) к высшему теоретическому (словесно-логическому).
Использование в обучении математики учебников Аргинской И. И. ведёт к интенсификации развития различных видов мышления младших школьников. Т.к. обеспечивается систематическая и целенаправленная работа учителя, направленная на выявление и применение оптимального содержания, форм и методов, способствующих положительной динамике развития мышления младших школьников от наглядно-действенного до словесно-логического; подбирается система заданий, воздействующая на всех детей: «визуалистов», «аудиолистов», «кинестетиков».
Работа по развитию различных видов мышления посредством обучения математике по учебникам Аргинской И. И. оказывает положительное влияние и на качество знаний учащихся по математике, повышает уровень математического образования младших школьников, развивает интерес к предмету, познавательную активность в обучении.
Так, н-р, учащиеся экспериментального класса на протяжении двух лет обучения занимают призовые места в школьных конкурсах по математике, получены лучшие результаты по школе в конкурсе «Русский медвежонок».
Качественная успеваемость по математике у учащихся экспериментального класса повышается, что отражено в графике.

Показатели выполнения задач повышенной трудности (по результатам контрольных работ) также повышаются и отличаются от результатов контрольного класса, о чём свидетельствует приведённые ниже график и таблица:
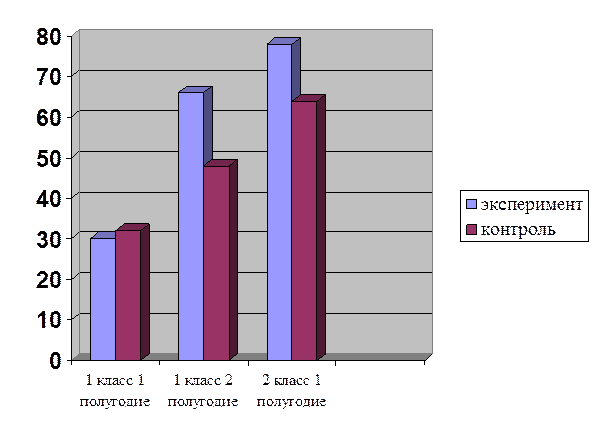
| 1 класс | 2 класс | ||
| 1 полугодие | 2 полугодие | 1 полугодие | |
| Экспериментальный класс | 30% | 66% | 78% |
| Контрольный класс | 32% | 48% | 64% |
Литература.
1.Безруких М.М., Ефимова С.П. Знаете ли вы своего ученика? М., 1991.
2.Выготский Л. С. Мышление и речь - М: Лабиринт 1996 г.
3.Выготский Л. С. Собрание сочинений в шестом томе – М - 1984 – т. 4 “Детская психология”.
4.Давыдов В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования – М: Педагогика, 1986 г.
5.Заика Е. В. Комплекс интеллектуальных игр для развития мышления учащихся, “Вопросы психологии” - 1990 г. № 6 .
6.Заика Е.В. и др. Об организации игровых занятий для развития мышления, памяти, воображения школьников // Вопросы психологии – 1995, №2.
7.Зак А. З. Развитие интеллектуальных способностей у детей 6 - 7 лет - М: Просвещение 1996 г.
8.Зак А. З. Развитие умственных способностей младших школьников - М: Просвещение 1994 г.
9.Зак А.З. Различия в мышлении детей. – М: Просвещение, 1992.
10.Занков Л.В. Избранные педагогические труды. - М., 1990.
11.Занков Л.В. Обучение и развитие. М., 1975.
12.Леонтьев А. Н.. Избранные психологические произведения: в 2т М: Педагогика , 1983 г. – т.1.
13.Люблинская А. А. Детская психология, - М: Просвещение, 1971г.
14.Матюшкин А.М. Психология мышления.
15.Мухина В. С. Детская психология - М: Просвещение, 1985 г.
16.Обухова Л.Ф. Этапы развития детского мышления. – М., 1981.
17.Овчинникова Т.Н. Личность и мышление ребёнка: диагностика и коррекция. – М.: Академический проект; Екатеринбург; Деловая книга, 2000.
18.Петровский А.В., Ярошевский М.Г. Психологический словарь. М., Издательство политической литературы, 1990.
19.Программы общеобразовательных учреждений. Начальные классы.
20.Рубинштейн С. А. Основы общей психологии в 2 т, т.1 - М: Педагогика 1989 г.
21.Тихомирова Л.Ф., Басов А.В. Развитие логического мышления детей. – Ярославль, 1995.
22.Тихомирова Л.Ф. Упражнения на каждый день. Логика для младших школьников: популярное пособие для родителей и педагогов. – Ярославль: «Академия развития», «Академия К». – 1998.
Хрестоматия по возрастной и педагогической психологии, - ч1 - М: Просвещение, 1980 г.
23.Чуприкова Н.И. Умственное развитие и обучение: Психологические основы развивающего обучения. - М., 1995.
Дата добавления: 2015-04-15; просмотров: 257; Мы поможем в написании вашей работы!; Нарушение авторских прав |