Примеры решения задач. Построить 3 проекции отрезка прямой АВ по заданным координатам точек: А (25,55,115) и В (150,5,45)

Задача 1 (Рисунок 1)

Построить 3 проекции отрезка прямой АВ по заданным координатам точек: А (25,55,115) и В (150,5,45)

Алгоритм решения:

1. Проводим оси координат X, Y, Z.

2. По заданным координатам строим 3 проекции точек А (А , А , А )

и В (В , В , В ).

3. Одноименные проекции точек А и В соединяем и получаем фронтальную (А В ), горизонтальную (А В ) и профильную (А В ) проекции отрезка прямой АВ.

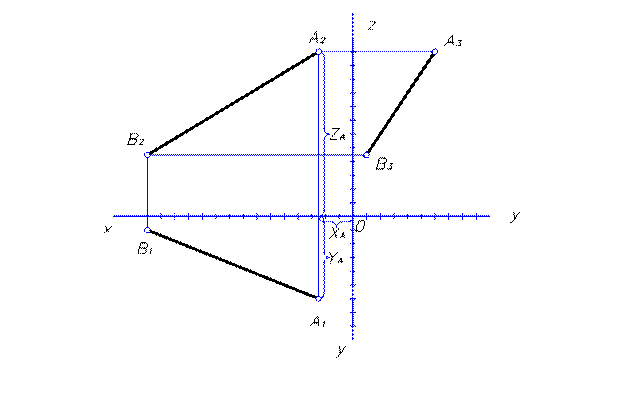
Рисунок 1
Задача 2 (Рисунок 2)

Построить 3 проекции точки С, расположенной относительно точки А левее на 65 мм, дальше на 45 мм и ниже на 15 мм. Построить три проекции точки D, расположенной относительно точки В правее на 45 мм, ближе на 45 мм и ниже на 35 мм.

Алгоритм решения:

1. Проводим вертикальную линию связи левее на 65 мм от вертикальной линии связи для точки А ( А А ).

2. От оси Х откладываем координаты Yc = Ya-45=55-45=10;

Zc = Za-15=115-15=100 и находим проекции точки С ( C ,С ,С ).

3. Аналогичным образом строим проекции точки D (D ,D ,D ).

Рисунок 2

Задача 3 (Рисунок3)

Через точку С провести прямую СF, параллельную прямой АВ

Алгоритм решения

1. Через горизонтальную проекцию точки С ( С ) проводим прямую С F , параллельную прямой А В .

2. Через фронтальную проекцию точки С ( С ) проводим прямую С F , параллельную прямой А В .

3. Через профильную проекцию точки С ( С ) проводим прямую С F ,

параллельную прямой А В .

4. Координаты точки F выбираем произвольно.

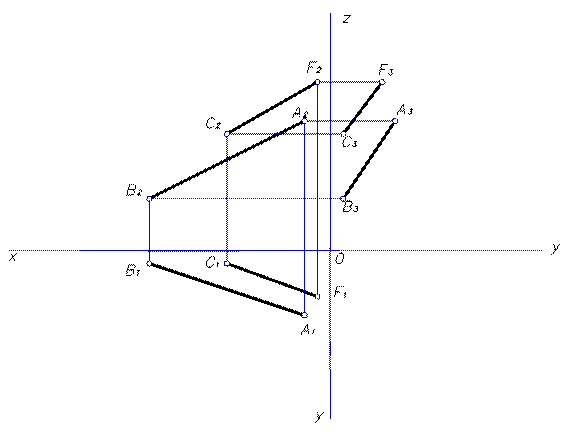Рисунок 3

Задача 4 (Рисунок4)

Через точку D провести прямую DE, параллельную плоскости проекций П₂ и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину.

Алгоритм решения:

1. Через горизонтальную проекцию точки D ( D ) проводим прямую D E , перпендикулярную вертикальным линиям связи , пересекая прямую А В в точке 1 (1 ).

2. Находим фронтальную проекцию точки 1 (1 ), для чего проводим вертикальную линию связи до пересечения с А В .

3. Соединяем фронтальную проекцию точки D (D ) с фронтальной проекцией точки 1 (1 ).

4. Ограничиваем прямую D1 точкой Е, которую выбираем произвольно.

5. Строим профильную проекцию прямой DE (D E ), проходящей через точку 1 (1 ) на прямой АВ (А В ).

6. Прямая DE называется фронтальной прямой уровня (фронталью).

7. Определяем натуральную величину прямой DE, для чего замеряем D E и записываем ее натуральную величину / DE / = 87.

Рисунок 4

Задача 5 (Рисунок5)

Определить взаимное положение прямых АВ и CD и доказать это на чертеже.

Алгоритм решения:

1. Взаимное положение прямых определяется с помощью конкурирующих точек.

2. В данном случае прямые АВ и CD называются пересекающимися, т.к. проекции их точки пересечения 2 ( 2 , 2 , 2 ) расположены на одной линии связи.

Рисунок 5

Задача 6 (Рисунок 6 )

Разделить прямую АВ точкой К в отношении АК : КВ = 5 : 2.

Алгоритм решения:

1. Из любого конца данного отрезка на любой проекции , например из А , проводим под произвольным острым углом вспомогательную прямую линию.

2. На этой линии от точки А циркулем откладываем 7 равных отрезков произвольной длины.

3. Крайнюю точку В последней отложенной части соединяем с В .

4. Находим точку К на расстоянии 5/7 от точки А .

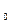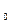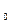5. Из точки К проводим К К параллельно В В .

6. Находим фронтальную К и профильную К проекции точки К.

Рисунок 6

Задача 7 (Рисунок 7 )

Пересечь прямую АВ фронтально проецирующей прямой MN.

Алгоритм решения:

1. Произвольно проводим горизонтальную проекцию прямой MN (M N ), совпадающую с вертикальной линией связи и пересекающую горизонтальную проекцию прямой АВ (А В ) в точке 3 (3 ).

2. Находим фронтальную проекцию точки 3 (3 ) на пересечении вертикальной линии связи с фронтальной проекцией прямой АВ (А В ). Фронтальные проекции точек M (M ) и N (N ) будут совпадать с фронтальной проекцией точки 3 (3 ).

3. Строим профильную проекцию прямой M N (M N ) через точку 3 (3 ), лежащей на прямой АВ (А В ).

4. Определяем видимость прямой MN (M N ) на фронтальной плоскости проекций. Точки M ,N ,3 - являются фронтально-конкурирующими. Видимой будет точка N, имеющая наибольшую координату по глубине.

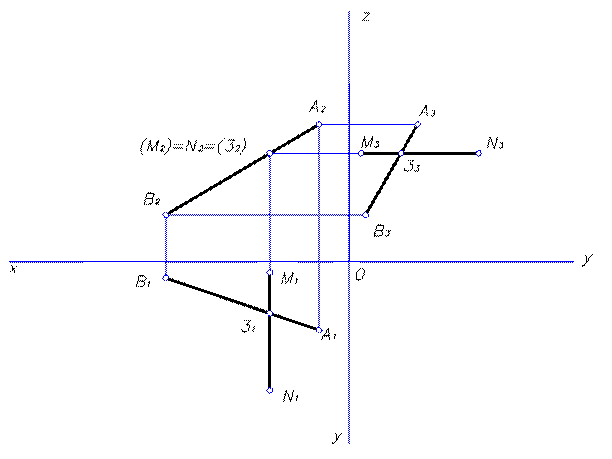Рисунок 7

Контрольные вопросы

1. Какой чертеж называется комплексным?

2. Как называются и обозначаются плоскости проекций?

3. Что такое линии связи на комплексном чертеже?

4. Как построить третью (профильную) проекцию точки?

5. В каком случае длина проекции отрезка равна длине самого отрезка?

6. В каком случае проекция прямой обращается в точку?

7. Какая прямая называется прямой общего положения?

8. Как по комплексному чертежу определить принадлежность точки прямой линии?

9. Какие прямые называются прямыми уровня? Как они обозначаются?

10. Что характерно для комплексного чертежа прямой уровня?

11. Какие прямые называются проецирующими? Как они обозначаются?

12. Какие точки называются конкурирующими? Как определить их видимость?

13. Как разделить отрезок в заданном отношении на комплексном чертеже?

14. Как могут располагаться в пространстве прямые по отношению

друг к другу?

15. Какие прямые называются:

а) параллельными?

б) пересекающимися?

в) скрещивающимися?

16. Как определить взаимное положение прямых по комплексному чертежу?

Рисунок 8 – Пример выполнения задания1

Задание 2 «Пересечение прямой с плоскостью»

Целевое назначение

Закрепить знания студентов по решению задач на взаимное расположение в пространстве прямой и плоскости.

Содержание задания

Построить точку пересечения прямой с плоскостью, заданной координатами точек. Определить видимость прямой относительно плоскости на всех проекциях.