Алгоритм решения. Задача решается способом секущих плоскостей

Задача решается способом секущих плоскостей. В нашем примере для построения линии пересечения рационально использовать горизонтальные плоскости уровня. Они рассекут конус и шар по окружностям, которые на плоскости П₁ изображаются без искажения.

1. Граница проведения секущих плоскостей определяется точками 1 и 2 (1₂ и 2₂), высшей и низшей точками линии пересечения. Первую секущую плоскость Г проведем через экватор шара. Она рассечет шар по окружности с радиусом R , а конус по окружности с радиусом R₁.

2. Строим горизонтальную проекцию сечения конуса. (Горизонтальная проекция сечения шара плоскостью Г совпадает с проекцией экватора). В пересечении контуров этих сечений (окружностей) получим горизонтальные проекции точек 3₁ и 4₁ линии пересечения. Эти точки одновременно являются и опорными. Они на горизонтальной проекции отделяют видимую часть линии пересечения от не видимой, т.к. лежат на экваторе шара. Фронтальные проекции этих точек находятся на плоскости Г (Г₂).

3. Для построения промежуточных точек в пределах высшей (1₂) и низшей (2₂) точек линии пересечения проводим целый ряд секущих плоскостей (Г₂¢, Г¢¢₂…), строим их сечения, в пересечении которых определяются искомые точки. В нашем примере построена лишь одна пара промежуточных точек.

4. Плавной кривой соединяем эти точки. Окончательную обводку делаем по лекалу.

5. На проекциях линии пересечения отмечаем точки 5, 6, 7 и 8 пересечения ближней и дальней образующей конуса с поверхностью шара, а также точки 9 и 10 пересечения второго главного меридиана сферы с поверхностью конуса, которые также являются опорными.

6. Видимость линии пересечения на горизонтальной и профильной проекции определяем по сфере. На горизонтальной проекции линия пересечения видна от точки 1(1₁) до точек 3(3₁) и 4(4₁), а далее от этих точек до точки 2(2₁) не видимая. Часть основания конуса (под сферой) изображается линией невидимого контура. На профильной плоскости проекций линия пересечения видна только от точки 1(1₃) до точек 9(9₃) и 10(10₃). Очерковый второй главный меридиан сферы обводим линией видимого контура от наивысшей точки до точек 9(9₃) и 10(10₃). Очерковые образующие конуса существуют от вершины S(S₃) до точек 5(5₃) и 6(6₃) и от основания до точек 7(7₃) и 8(8₃). Часть образующих конуса (за сферой) изображаем линиями невидимого контура.

Контрольные вопросы

1. Сформулируйте правило построения линии взаимного пересечения поверхностей многогранников.

2. Сформулируйте правило построения линии взаимного пересечения многогранника с поверхностью вращения.

3. Сформулируйте правило построения линии взаимного пересечения поверхностей вращения.

4. Сущность метода вспомогательных плоскостей.

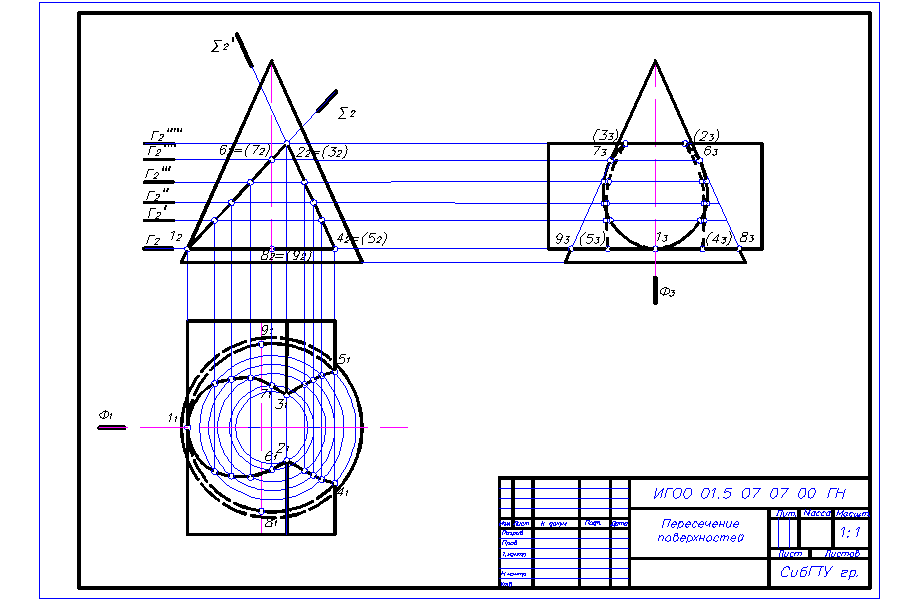
Рисунок 27 – Пример выполнения листа 1 задания 5

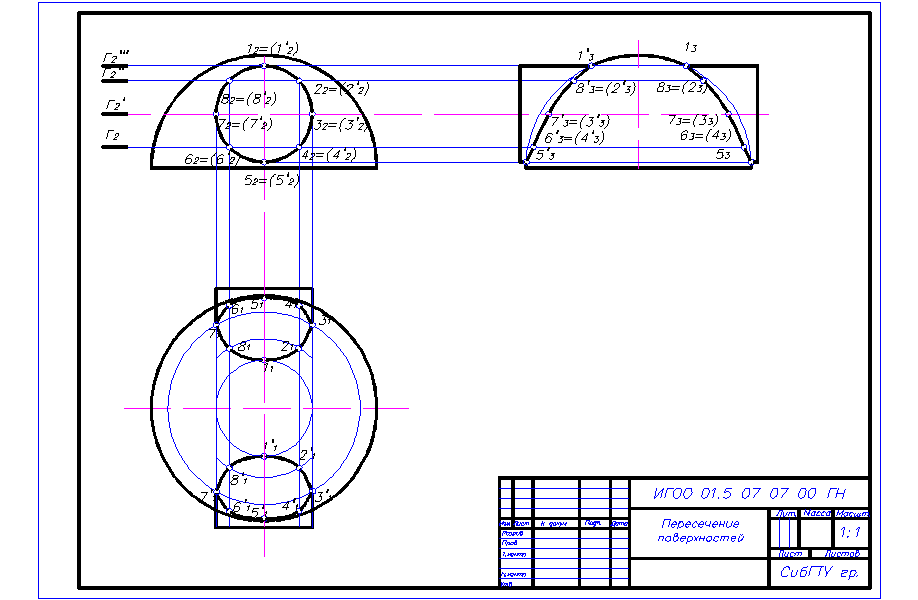
Рисунок 28 – Пример выполнения листа2 задания 5